Shapes
Dice come in a variety of shapes. Shapes of mathematically fair dice are called isohedra, which are convex polyhedra with special properties. Other dice are based on barrels (prisms and antiprisms) and spheres.

In the sequel we use the following structure to group the various dice shapes:
- Fair Dice: Numbered shapes with equal probability of being rolled
- Isohedra: Convex polyhedra with symmetries acting transitively on its faces
i. Platonic Solids: Convex polyhedra with equivalent faces composed of congruent convex regular polygons.
ii. Catalan Solids: Dual polyhedra of the Archimedean solids; their faces are not regular polygons.
iii. Dipyramids: Two pyramids symmetrically placed base-to-base.
iv. Trapezohedra: Dual polyhedra of the Archimedean antiprisms, composed symmetrically staggered congruent deltoids (or kites).
v. Special Isohedra: Convex polyhedra with symmetries w.r.t an even number of faces, created by skewing platonic solids, catalan solids, dipyramids, and trapezohedra.
- Curved Surfaces: Although not commonly mentioned, there are a few fair dice with curved surfaces
i. Sphere: A shapes with a single face
ii. Lens: A fair binary die
iii. Edged cigar shapes: Prisms that taper in both ends, with N-sided cross sections. Allows to make fair dice with an odd number of faces
- Instable Surfaces: Some potentially unfair dice can be turned into fair dice by modifiying them in a way that the unfair faces become instable
i. Modified Prisms: Prisms with two regular short n-pyramids (or some round shapes) on each of the base polygons. Allows to make fair dice with an odd number of faces
ii. Modified Antiprisms: Antiprisms with two regular short n-pyramids (or some round shapes) on each of the base polygons
iii. Special dice with instable surfaces
To be added
o Convex envelope
o Polyisohedra
o Dice with movable parts
o Dice in dice
Fair Dice
We use the following definition of a fair die: A fair die is a shape that is labelled such that each label has an equal probability of coming up when the shape is tossed onto a flat surface, regardless of the materials used and the angle, spin and speed with which the shape is tossed.
Commonly, only isohedra are considered to be shapes that make fair die. Here we also include shapes with curved surfaces, dice with instable surfaces, dice with an isohedral convex envelope and dice with movable parts (like spherical dice with an internal cavity and a weight) and dice in dice.
Isohedra
Due to the importance of Isohedra, there is a special section with more details here.
An isohedron is a convex polyhedron with symmetries acting transitively on its faces. Every isohedron has an even number of faces. The isohedra make fair dice, and there are 30 of them (25 finite solids and 5 classes of infinite solids):
- Platonic solids (5 finite solids)
- Catalan solids (13 finite solids of which only 11 are suitable as dice)
- Dipyramids (a class of infinite solids)
- Trapezohedra (a class of infinite solids)
- Special Isohedra (7 finite solids and 3 classes of infinite solids)
All isohedra can be used as fair dice if the rolled number is the one marked on the face a die lands on. However, this is not practical: the number is not visible and lifting a die to show the rolled number invites cheating. Therefore, normally, the rolled number is the one painted “on top”, assuming that there are parallel faces on a die. This holds for the following dice
- Platonic solids: Hexahedron, Cube (D6), Regular Octahedron (D8), Regular Dodecahedron (D12), Icosahedron (D20)
- Catalan solids: Rhombic Dodecahedron (D12), Small Triakis Octahedron (D24), Tetrakis Hexahedron (D24), Deltoidal Icositetrahedron (D24), Rhombic Triacontahedron (D30), Disdyakis Dodecahedron (D48), Deltoidal Hexecontahedron (D60), Triakis Icosahedron (D60), Pentakis Dodecahedron (D60), Disdyakis Triacontahedron (D120)
- Dipyramids with 4n faces
- Trapezohedra with 4n+2 faces
- None of the Special Isohedra, except
- a special version of the D8 Octahedral Pentagonal Dodecahedron (Pyritohedron)
- Dyakis Dodecahedron (D24)
- are there other exceptions? (to be verified)
For some dice a numbering scheme can be chosen that allows a clear identification of the rolled number:
- Regular Tetrahedron (D4): The number of faces is identical to the number of vertices (4), and there is always a vertex opposite a face. Hence, the vertices can be marked. Alternatively, the edges adjacent to a face can be marked (3 each with the same number). There is a version with an outer tetrahedron grid and an inner tetrahedron with parallel faces (see below)
- Isosceles Tetrahedron (D4) and Scalene tetrahedron (D4): The number to be read is that on the face whose short edge lies on the ground
- Triakis Tetrahedron (D12): A numbering scheme was suggested by Mitchel D Klink of the Bone Rollers’ Guild [7]. When one side is face-down, the feature that actually points upward is an edge shared by two triangular faces, positioned so that the vertex at one end sits higher than the other. If the numbers on the faces are placed in one of the acute angles, the number that sits highest can be read as the result of its rolls. His design is now available on Shapeways.
- Dipyramids with 4n+2 faces and Trapezohedra with 4n faces: There is always a parallel edge opposite a faces, hence the edges can be marked
- Tetragonal Scalenohedron (D8), a skewed dipyramid: The number to be read is that on the face which doesn't touch ground.
For some special isohedra with up to, say, 12 faces it is possible to identify the rolled number on the face on top which is almost parallel to the ground, see e.g. the Deltoidal Dodecahedron (D12) below.
There is no known numbering scheme that allows a clear identification of the rolled number for the Pentagonal Icositetrahedron (D24) and the Pentagonal Hexecontahedron (D60). Therefore, these isohedra are not suitable for dice.
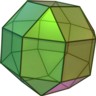
Platonic Solids
Platonic Solids are congruent are convex polyhedra with equivalent faces composed of congruent convex regular polygons. There are exactly five such solids: the cube (6 faces), dodecahedron (12), icosahedron (20), octahedron (8), and tetrahedron (4).
|
Regular Tetrahedron (D4) |
|
|
Composed of four equivalent equilateral triangular faces with four vertices and six edges.
One type of vertex with 3 edges.
The tetrahedron is also a degenerate antiprism of 2 sides.
No parallel faces. Therefore, either the edges or the vertices are marked with numbers. |
|
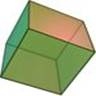
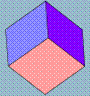
Hexahedron, Cube (D6) |
|
|
Composed of six square faces that meet each other at right angles with eight vertices and 12 edges.
One type of vertex with 3 edges.
The cube is also a square prism. |
|
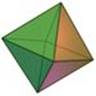
Regular Octahedron (D8) |
|
|
Composed of eight equivalent equilateral triangular faces with six vertices and 12 edges.
One type of vertex with 4 edges.
The octahedron of unit side length is the antiprism of three sides. The octahedron is also a square dipyramid with equal edge lengths. |
|
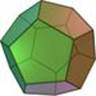
Regular Dodecahedron (D12) |
|
|
Composed of 12 regular pentagonal faces with 20 vertices and 30 edges.
One type of vertex with 3 edges.
|
|
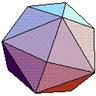
Icosahedron (D20) |
|
|
Composed of 20 equivalent equilateral triangular faces with 12 vertices and 30 edges.
One type of vertex with 5 edges.
|
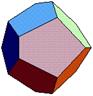
Catalan Solids
Catalan Solids are dual polyhedra of the Archimedean solids, and their faces are not regular polygons. They are named in honor of the Belgian mathematician Eugène Charles Catalan who first published them in 1862. There are 13 Catalan solids with 12, 24, 30, 48, 60, and 120 faces. Only 11 of those are suitable as dice (all except the pentagonal icositetrahedron and the pentagonal hexecontahedron)
|
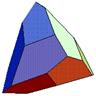
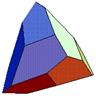
Triakis Tetrahedron (D12) |
Bone Roller / Shapeways |
Non-regular dodecahedron composed of 12 isosceles triangular faces with eight vertices and 18 edges.
Can be constructed by cumulation of a unit edge-length tetrahedron by a pyramid with height sqrt(6)/15.
Two types of vertices with 3 and 6 edges each.
No parallel faces. A numbering scheme suggested by Mitchel D Klink allows that the number that sits highest can be read as the result.
Dual polyhedron of the truncated tetrahedron. |
|
|
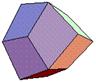
Rhombic Dodecahedron (D12) |
AskAstro
Justin Michell
DiceLab |
|
Composed of 12 rhombic faces with 14 vertices and 24 edges.
Can be constructed by affixing a square pyramid of height 1/2 on each face of a unit edge-length cube.
Two types of vertices with 3 and 4 edges each.
Dual polyhedron of the cuboctahedron.
|
|
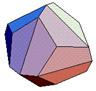
Triakis Octahedron (D24) |
friz / Shapeways |
Composed of 24 isosceles triangular faces with 14 vertices and 36 edges.
Can be constructed by cumulation of a unit edge-length octahedron by a pyramid with height sqrt(3)-2/3*sqrt(6).
Two types of vertices with 3 and 8 edges each.
Dual polyhedron of the truncated cube.
|
|
|
Tetrakis Hexahedron (D24)
|
Koplow
GameScience |
Composed of 24 isosceles triangular faces with 14 vertices and 36 edges.
Can be constructed by cumulation of a unit cube by a pyramid with height 1/4.
Two types of vertices with 4 and 6 edges each.
Dual polyhedron of the truncated octahedron. |
|
|
Deltoidal Icositetrahedron (D24) |
Franck Dutrain D-Total Alexander Simkin / GameScience
DiceLab |
Composed of 24 deltoidal faces with 26 vertices and 48 edges.
Also called trapezoidal icositetrahedron.
Three types of vertices with 3, 4 and 4 edges each.
Dual polyhedron of the small rhombicuboctahedron.
|
|
|
Pentagonal Icositetrahedron (D24) Not suitable for dice! |
friz / Shapeways |
Composed of 24 irregular pentagonal faces with 38 vertices and 60 edges.
Comes in two enantiomorphous forms, known as laevo (left) and dextro (right).
Dual polyhedron of the snub cube.
No parallel faces, rolled number is not clearly identifiable à this shape is not suitable for dice. |
|
|
Rhombic Triacontahedron (D30) |
Armory
Koplow
DiceLab |
Composed of 30 rhombic faces with 32 vertices and 60 edges.
Two types of vertices with 3 and 6 edges each.
Dual polyhedron of the icosidodecahedron.
|
|
|
Disdyakis Dodecahedron (D48) |
|
Composed of 48 triangular faces with 26 vertices and 72 edges.
Also called Hexakis Octahedron.
Three types of vertices with 4, 6 and 8 edges each.
Dual polyhedron of the Archimedean great rhombicuboctahedron.
|
|
|
Deltoidal Hexecontahedron (D60) |
friz / Shapeways |
Composed of 60 deltoidal faces with 62 vertices and 120 edges.
Also called trapezoidal hexecontahedron or strombic hexecontahedron.
Three types of vertices with 3, 4 and 5 edges each.
Dual polyhedron of the small rhombicosidodecahedron. friz / Shapeways
|
|
|
Pentagonal Hexecontahedron (D60) Not suitable for dice! |
friz / Shapeways |
Composed of 60 irregular pentagonal faces with 92 vertices and 150 edges.
Comes in two enantiomorphous forms, known as laevo (left) and dextro (right).
Dual polyhedron of the snub dodecahedron
No parallel faces, rolled number is not clearly identifiable à this shape is Not suitable for dice. |
|
|
Triakis Icosahedron (D60) |
friz / Shapeways |
Composed of 60 isosceles triangular faces with 32 vertices and 90 edges.
Can be constructed by cumulation of a regular icosahedron by a pyramid.
Two types of vertices with 3 and 10 edges each.
Dual polyhedron of the truncated dodecahedron |
|
|
Pentakis Dodecahedron (D60) |
friz / Shapeways |
Composed of 60 isosceles triangular faces with 32 vertices and 90 edges.
Can be constructed by cumulation of a regular dodecahedron by a pentagonal pyramid.
Two types of vertices with 5 and 6 edges each.
Dual polyhedron of the truncated icosahedron. |
|
|
Disdyakis Triacontahedron (D120) |
friz / Shapeways |
Composed of 120 irregular triangular faces with 62 vertices and 180 edges.
Also known as the hexakis icosahedron.
Three types of vertices with 4, 6 and 10 edges each.
Dual polyhedron of the Archimedean great rhombicosidodecahedron.
Largest non-bi-polar fair die. |
Dipyramids
Dipyramids are also called bipyramids or basic triangular dihedral. An infinite number of solids can be created by placing two pyramids symmetrically base-to-base. The height is arbitrary. A dipyramid whose base is a regular n-sided polygon is composed of 2n identical isosceles triangular faces with n+2 vertices and 3n edges.
The dipyramids are duals of the regular prisms.
In order to end up with opposite pairs of faces for convenient numbering, there need to be an even number of faces on each side of the "equator", such that n has to be even (n=2m). Then, the total number of faces is 2n=4m, m>1. (If dipyramids with odd n>1 are chosen, the numbers have to be printed at the edges).
|
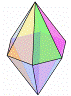
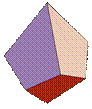
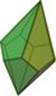
Triangular Dipyramid (D6) |
friz / Shapeways |
|
n=3, base is a triangle, six faces, five vertices, and nine edges.
Two tetrahedra placed symmetrically base-to-base.
Numbers are printed on the edges |
|
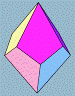
Square Dipyramid (D8) |
TSR
|
n=4, base is a square, eight faces, six vertices, and twelve edges.
Regular octahedron, all edges are of same length (top)
Elongated octahedron (bottom) |
|
|
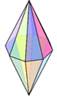
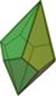
Pentagonal Dipyramid (D10) |
friz / Shapeways
friz / Shapeways |
n=5, base is a regular pentagon, 10 faces, seven vertices, and 15 edges.
Regular pentagonal dipyramid, all edges are of same length (top)
Elongated pentagonal dipyramid (bottom)
Numbers are printed on the edges |
|
|
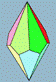
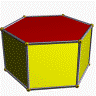
Hexagonal Dipyramid (D12) |
friz / Shapeways
Loki3 / Shapeways
Roll to Riches |
n=6, base is a regular hexagon, 12 faces, eight vertices, and 18 edges. |
|
|
Octagonal Dipyramid (D16) |
|
n=8, base is a regular octagon, 16 faces, 10 vertices, and 24 edges. |
|
|
Octadecagonal Dipyramid (D36) |
|
|
n=18, base is a regular octadecagon, 36 faces, 20 vertices, and 54 edges. |
Trapezohedra
Trapezohedra (also called antidipyramids or deltohedra) are the dual polyhedra of the Archimedean antiprisms. (The name for these solids is not particular well chosen since their faces are not trapezoids but deltoids).
The n-gonal trapezohedron (n>2) is composed of 2n faces which are congruent deltoids (or kites) with 2n+2 vertices and 4n edges. The faces are symmetrically staggered. The n-gon part of the name does not reference the faces here but arrangement of vertices around an axis of symmetry.
In order to end up with opposite pairs of faces for convenient numbering, there need to be an odd number of faces on each side of the zig-zagged "equatorial" line, such that n has to be odd (n=2m-1). Then, the total number of faces is 2n=4m-2, m>1. (If trapezohedra with even n are chosen, the numbers have to be printed at the edges).
There are two types of vertices, the ones on the “equatorial line” with 3 edges each and the two at the poles with n edges each.
|
Trigonal Trapezohedron (D6) |
friz / Shapeways
friz / Shapeways
Wikicommons, own foto pending
DiceLab
|
|
n=3, six faces, eight vertices, and 12 edges. A cube is a special case trigonal trapezohedron with square faces, and there are also versions with rhombi and irregular quadrilaterals.
It can be proven (friz) that there is no trigonal trapezohedron with deltoids. |
|
Tetragonal Trapezohedron (D8) |
friz / Shapeways |
|
n=4, eight faces, ten vertices, and 16 edges.
Numbers are printed on edges.
Two types of vertices with 3 and 4 edges each.
|
|
Pentagonal Trapezohedron (D10) |
|
n=5, ten faces, 12 vertices, and 20 edges.
Top: all vertices normal
Center: top and bottom vertices blunt
Bottom: center vertices blunt |
|
|
Hexagonal Trapezohedron (D12) |
|
n=6, twelve faces, 14 vertices, and 24 edges.
Numbers are printed on edges |
|
|
Heptagonal Trapezohedron (D14) |
GameScience
|
|
n=7, 14 faces, 16 vertices, and 28 edges
|
|
Enneagonal Trapezohedron (D18) |
Paper model, missing in my collection [1] |
|
n=9, 18 faces, 20 vertices, and 36 edges |
|
Trisdecagonal Trapezohedron (D26) |
Sean Michael Ragan / Shapeways |
|
n=13, 26 faces, 28 vertices, and 52 edges |
|
Heptadecagonal Trapezohedron (D34) |
Chessex |
|
n=17, 34 faces, 36 vertices, and 68 edges
|
|
Icosikaipentagonal Trapezohedron (D50) |
GameScience |
|
n=25, 50 faces, 52 vertices, and 100 edges
|
Special Isohedra
There are seven more solids which can be created by skewing platonic solids, and catalan solids, and three infinite classes of skewed dipyramids (2) and trapezohedra (1). They are convex with symmetries w.r.t an even number of faces.
|
Isosceles Tetrahedron (D4) |
|
|
Composed of four identical isosceles triangular faces with four vertices and six edges.
Tetragonal Disphenoid.
No parallel faces, but the number to be read is that on the visible face whose short edge lies on the ground. |
|
Scalene tetrahedron (D4) |
friz / Shapeways |
|
Composed of four identical scalene triangular faces with four vertices and six edges.
No parallel faces, but the number to be read is that on the visible face whose short edge lies on the ground. |
|
Skewed Trigonal Trapezohedron (D6) |
|
|
Composed of six irregular quadrilaterals |
|
Octahedral Pentagonal Dodecahedron (D12)
|
friz / Shapeways |
|
Composed of 12 irregular pentagonal faces with 20 vertices and 30 edges.
Skewed dodecahedron which has a symmetry that mirrors the octahedron. |
|
Tetragonal Pentagonal Dodecahedron (D12)
|
loki3 / Shapeways
|
|
Composed of 12 irregular pentagonal faces with 20 vertices and 30 edges.
Skewed dodecahedron which looks similar to the Tetrahedron.
No parallel faces, but rolled number is clearly identifiable. The design by loki3 consists of a wireframe with embedded parallel sides. From the right viewing angle it is possible to see both 12 (left) and 1 (right). |
|
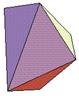
Deltoidal Dodecahedron (D12) |
SirisC, Shapeways
friz / Shapeways |
|
Composed of 12 identical deltoidal faces with 14 vertices and 24 edges.
Skewed version of the rhombic dodecahedron.
No parallel faces, but rolled number is clearly identifiable |
|
Hexakis Tetrahedron (D24) |
|
|
Aka Hextetrahedron.
Composed of 24 scalene triangular faces with 14 vertices and 36 edges.
Three types of vertices with 4, 6 and 6 edges each.
No parallel faces, but rolled number is identifiable.
Can be made by changing the length of the face axes and edge-midpoint axes of a tetrahedron (loki3)
|
|
Dyakis Dodecahedron (D24) |
friz / Shapeways |
|
Composed of 24 irregular tetragonal faces with 26 vertices and 48 edges.
Can be constructed by warping the dodecahedron in such a way that each face folds in half. |
|
Triangular Dihedron skewed up/down (D4n) |
friz / Shapeways DiceLab
|
|
Can be constructed by skewing the equatorial vertices of a dipyramid with 4n faces up and down Example: D8, Tetragonal Scalenohedron
No parallel faces, i.e. from the right viewing angle it is possible to see both 8 (left) and 1 (right). |
|
Triangular Dihedron skewed in/out (D4n) |
friz / Shapeways |
|
Can be constructed by squeezing the equatorial vertices of a dipyramid with 4n faces in and out from the center of the solid. Example: D16 Skewed Octagonal Triangular Dihedron |
|
Skewed Deltoidal Dihedron (D2n) |
friz / Shapeways
friz / Shapeways |
|
Can be constructed by grasping a deltohedron by two opposing vertices and stretching it, to form an elongated solid whose sides are all of equal length, and then twisting it a bit, so the sides become uneven. Examples: D6 Trigonal Trapezohedron (top) D12 Hexagonal Trapezohedron (bottom) |
Curved surfaces
There are three shapes of fair dice with curved surfaces [4]
Sphere
|
Sphere (D1) |
|
The sphere is a solid with a single face. |
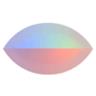
Lens
|
Lens (D2) |
|
|
The lens is a solid with two faces. |
Edged cigar shapes
The shape of these dice are prisms that taper in both ends, with N-sided cross sections. This is the only way to make fair dice with an odd number of
faces (not counting the sphere).
|
Square Edged Cigar (D4) |
Football Fever |
|
4-sided prism that tapers in both ends |
|
Hexagonal Edged Cigar (D6) |
Football Fever
Hasbro / Monopoly
|
|
6-sided prism that tapers in both ends |
|
Decagonal Edged Cigar (D10) |
GRIDIRON MASTER / PHI SPORTS |
|
10-sided prism that tapers in both ends |
Isohedral Convex Envelope
This section shows dice with an isohedral convex envelope. They are fair.
|
Regular Tetrahedron (D4) |
Magic / Shapeways |
Tetrahedron.
There are no parallel faces. This design consists of a wireframe with embedded parallel sides. |
|
|
Pentagonal Trapezohedron (D10) |
Magic / Shapeways |
Dodecahedron with “axis”. Convex envelope is a pentagonal trapezohedron
|
|
|
Tetragonal Pentagonal Dodecahedron (D12)
|
loki3 / Shapeways |
|
Skewed dodecahedron which looks similar to the Tetrahedron.
There are no parallel faces. This design consists of a wireframe with embedded parallel sides. |
Instable Surfaces
Some basically unfair shapes can be turned into fair dice by modifying them in a way that the unfair faces become instable such that a die can land only on fair stable faces. Examples include “crystal dice” and barrel-type dice.
Modified Prisms
An n-sided right prism is a polyhedron composed of two parallel copies of a regular n-sided polygon, connected by a band of 2n rectangles. The joining edges and faces are perpendicular to the base faces. An n-sided prism is composed of n+2 faces, 2n vertices and 3n edges.
The dual of a right prism is a dipyramid. The only fair die that is a prism is the cube.
|
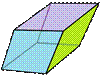
Square prism (D6) |
|
|
The cube is an equilateral square prism.
It is the only fair prism. |
However, prisms can be modified and hence turned into fair dice by making sure that they never land on its “poles” (the top or bottom face). This is typically done by putting two regular short n-pyramids (or some round shapes) on each of the base polygons. If these pyramids are short enough such that their faces are instable, we get a die which will always “land” on one of the n rectangles. Since these rectangles are all equal, this die can be considered fair.
Because all isohedra have an even number of faces, these modified prisms are the only way to make “almost” fair dice with an odd number of faces.
|
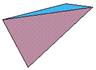
Rounded-off |
GameScience
Crystal Caste |
|
Rounded-off elongated right triangular prism.
The die “lands” on each of the three faces with equal probability.
Numbers are printed on (GameScience) or near (Crystal Caste) the edges or on angled the end faces (DiceLab).
The DiceLab design (center of gravity) makes it impossible to settle on an end face. |
|
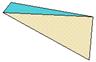
Pyramidal
|
Crystal Caste
Bear Cub Machine |
|
Elongated right square prism with two square pyramids.
The die “lands” on each of the four rectangles with equal probability |
|
Rounded-off Hexagonal Prism (D6) |
Acorn Die / Matt Bowman |
|
Rounded-off elongated right hexagonal prism.
The die “lands” on each of the six faces with equal probability. |
|
Modified Heptagonal Prism (D7) |
Odd Dice shop / Shapeways |
|
Elongated right heptagonal prism with two pyramids.
The die “lands” on each of the seven rectangles with equal probability
No parallel faces.
The roll is the total of the pips on the two uppermost faces
|
|
Modified Octagonal Prism (D8) |
Odd Dice shop / Shapeways |
|
Elongated right heptagonal prism with two pyramids.
The die “lands” on each of the seven rectangles with equal probability
The roll is the total of top three faces. Only every other face has a number. |
|
Modified Decagonal Prism (D10) |
Bear Cub Machine |
|
Elongated right decagonal prism with two “cones”.
The die “lands” on each of the ten rectangles with equal probability |
|
Modified Enneagonal Prism (D11) |
Odd Dice shop / Shapeways |
|
Elongated right Enneagonal prism with two pyramids.
The die “lands” on each of the eleven rectangles with equal probability.
No parallel faces.
The roll is the total of the pips on the two uppermost faces |
Modified Antiprisms
An n-sided right antiprism is a polyhedron composed of two parallel copies of a regular n-sided polygon (twisted by an angle 180°/n), connected by an
alternating band of 2n isosceles triangles. The line connecting the base centers is perpendicular to the base planes. An n-sided antiprism is composed of n+2 faces, n vertices and 2n edges.
Antiprisms are similar to prisms except the bases are twisted relative to each other, and that the side faces are triangles, rather than quadrilaterials: the vertices are symmetrically staggered.
The duals of the antiprisms are the trapezohedra. The only fair dice that are antiprisms are the tetrahedron (a degenerate 2-antiprism) and the octrahedron (3-antiprism with equilateral triangles).
|
2-Antiprism (D4) |
|
|
The tetrahedron is a degenerate antiprism: the polygon at the top and the bottom are degenerated to lines
|
|
3-Antiprism (D8) |
|
|
The octahedron is a 3-antiprism with eight equilateral triangles |
However, antiprisms can be modified and hence turned into fair dice by making sure that they never land on their “poles” (the top or bottom face). This is typically done by putting two regular short n-pyramids (or some round shapes) on each of the base polygons. If these pyramids are short enough such that their faces are instable, we get a die which will always “land” on one of the 2n triangles. Since these triangles are all equal, this die can be considered fair.
|
Modified
|
Monopoly Millennium Die
Crystal Caste |
|
Right 3-Antiprism with two triangular pyramids
The die “lands” on each of the six larger isosceles triangles with equal probability
|
|
Modified
|
Crystal Caste |
|
Right 4-Antiprism with two square pyramids.
The die “lands” on each of the eight larger isosceles triangles with equal probability |
|
Modified
|
Crystal Caste |
|
Right 5-Antiprism with two pentagonal pyramids.
The die “lands” on each of the ten larger isosceles triangles with equal probability.
The arrangement of the faces corresponds to an “elongated icosahedron”. |
|
Modified
|
Crystal Caste |
|
Right 6-Antiprism with two hexagonal pyramids.
The die “lands” on each of the twelve larger isosceles triangles with equal probability |
|
Modified
|
Crystal Caste |
|
Right 10-Antiprism with two decagonal pyramids.
The die “lands” on each of the twenty larger isosceles triangles with equal probability
|
Other Dice with Instable Surfaces
|
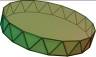
Rounded Trapezohedron (Dn) |
|
sphere
|
Also known as “cone” or “parachute”. Consists of an n-sided pyramid whose base is replaced by a half-sphere. Example is a D13 by DiceLab |
Unfair dice
Prisms
As seen above, n-sided prisms with n+2 faces do not make fair dice (except the cube) if no means are taken to make sure that they do not land on their “poles” (top or bottom surfaces). Still, there are some prism based dice being manufactured.
|
Triangular Prism (D5) |
GameScience |
Triangular right prism with numbers on the two base triangles and on the perpendicar edges.
This die does not “land” on all faces with equel probabilities, i.e., it is not fair. |
|
|
Pentagonal Prism (D7) |
GameScience |
|
Pentagonal right prism with numbers on the two base pentagons and on the perpendicar edges.
This die does not “land” on all faces with equal probabilities, i.e., it is not fair. |
|
Heptagonal Prism (D9) |
Missing in my collection [1] |
Heptagonal right prism.
This die does not “land” on all faces with equal probabilities, i.e., it is not fair. |
The longer the prism (compare to its „diameter“), the less likely it is that it lands on its poles. However, such dice can not be considered fair if that probability is not zero.
|
Elongated |
HABA Schleckermaul
Abraham Neddermann |
|
Elongated right triangular prism.
The die “lands” on each of the three faces with equal probability.
Numbers are printed on the faces or on the edges |
|
Elongated Pentagonal Prism (D5) |
Abraham Neddermann |
|
Elongated right pentagonal prism
The die “lands” on each of the five rectangles with equal probability. Numbers are printed on the edges. |
|
Elongated Heptagonal Prism (D7) |
Abraham Neddermann |
|
Elongated right heptagonal prism.
The die “lands” on each of the seven rectangles with equal probability.
Numbers are printed on the edges. |
|
Elongated Nonagonal Prism (D9) |
Abraham Neddermann |
|
Elongated right nonagonal prism.
The die “lands” on each of the nine rectangles with equal probability.
Numbers are printed on the edges. |
|
Elongated Hendecagonal Prism (D11) |
Abraham Neddermann |
|
Elongated right hendecagonal prism.
The die “lands” on each of the eleven rectangles with equal probability.
Numbers are printed on the edges. |
|
Elongated Tridecagonal Prism (D13) |
Abraham Neddermann |
|
Elongated right tridecagonal prism.
The die “lands” on each of the thirteen rectangles with equal probability.
Numbers are printed on the edges. |
|
Elongated Pentadecagonal Prism (D15) |
Abraham Neddermann |
|
Elongated right pentadecagonal prism.
The die “lands” on each of the fifteen rectangles with equal probability.
Numbers are printed on the edges. |
Truncated Polyhedra
|
Truncated Tehrahedron D4 |
DiceLab |
The numbers can face straight up, but it can land on a small triangular face, which DiceLab found happens about 3% of the time |
|
|
Truncated Octahedron D8 |
|
This is a space-filling polyhedron that can land on a square face, which DiceLab found happens about 2% of the time. |
Spheres
Some dice are made of spherical shapes. Here we show some mass produced spherical dice. There is a variety of designs available from Shapeways, shown in a special section with more details here.
|
Spherical D4 |
|
|
Colours instead of numbers. Easier to roll than a tetrahedron |
|
Spherical D6 Plastic |
|
Spherical die with internal cavity (in theory an octahedron, the dual of the cube) in which a weight moves which causes the die to settle in one of six orientations when rolled. |
|
|
Spherical D6 Wood |
|
|
Hollow, with internal cavity. |
|
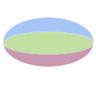
Flattened Spherical D6 |
Bo-Jo dice |
|
Flattened spherical D6 |
|
Flattened Spherical D7 |
Magic / |
Intersecting polyhedron |
Symmetry type C3v (3-fold pyramidal symmetry)
No parallel faces |
|
Flattened Spherical D8 |
|
|
Flattened spherical D8. Pipped, 2..9 |
|
Flattened Spherical D14 |
Magic /
Card Dice
|
|
Intersection of a cuboctahedron and a sphere.
Symmetry types Oh (full octahedral symmetry) and Td (full tetrahedral symmetry)
|
|
Flattened Spherical D18 |
Magic / |
|
Intersection of the squares of Rhombicuboctahedron and a sphere (there are 18 squares; the 8 triangles are not used)
Symmetry type Oh (full octahedral symmetry)
All faces are parallel. |
|
Flattened Spherical D22 |
Magic / |
|
Symmetry type D5d (5-fold antiprismatic symmetry)
|
|
Flattened Spherical D32 |
Glass, made in former Czechoslovakia |
|
Flattened Glass sphere, numbered 00,0,1..30 |
|
Flattended Spherical D50 |
Alan Davies |
|
Flattened plastic sphere
Symmetrical construction with 6-fold rotational symmetry: 1+6+12+12+12+6+1.
Symmetry type D6h (6-fold prismatic symmetry)
Numbered 0 (empty),1..49 |
|
Flattended Spherical D50 |
WMF
|
|
Symmetrical construction with 4-fold rotational symmetry: 1+4+4+4+8+8+8+4+4+4+1
Symmetry type D4h (4-fold prismatic symmetry)
Numbered 1..49 plus symbol WMF (0 or 50). Used for German Lotto with numbers 1..49. |
|
Zocchihedron (D100) |
GameScience |
|
Zocchihedron is the trademark of the most common 100-sided die, which was invented by Lou Zocchi, and debuted in 1985. It is not a polyhedron. Rather, it is more like a ball with 100 flattened planes. It is not fair.
|
Other Shapes
Various
|
D2 |
Bear Cub Machine |
|
“Coin”
|
|
D6 |
|
|
Concave , a.k.a “Bones”
|
|
D6 |
|
|
Crooked |
|
D6 |
|
|
Jumping
|
|
D6 |
|
|
Elliptical |
|
D6 |
|
|
Tactile |
|
D10 |
|
|
Truncated octahedron, Top: Blue Japanese “Trinity” die, numbered 0..9 Bottom: unknown white die, numbered 0..9 |
Rattling Bones
A truly unique design made by clsn / Shapeways. “Each die is realized by a skeleton (with a Platonic convex hull) with a wireframe model of the dual of the relevant polyhedron surrounding the skeleton. The numerals are affixed to the wireframe, which is free to move around on the skeleton--but not too far. Hence the name rattling bones. (The d4 is a little different; the numbers are on the ends of the skeleton)”





Printed in White Strong & Flexible material. D6 was manually inked.
References
- [1] Huge collection of shapes, including some paper models and prototypes not commercially available: http://www.dicecollector.com/diceinfo_how_many_shapes.html
- [2] 3D pictures of isohera: http://mathworld.wolfram.com/Isohedron.html
- [3] Wikipedia http://wikipedia.org/
- [4] Mathematical derivation of all fair dice: http://web.archive.org/web/20080501074022/http://hjem.get2net.dk/Klaudius/Dice.htm (was: http://hjem.get2net.dk/Klaudius/Dice.htm ). Click here for a local copy in PDF format.
- [5] Another mathematical derivation of all fair dice: http://dicephysics.info/thesis7.doc. Click here for a local copy in PDF format.
- [6] Detailed description of all fair dice: http://www.mathpuzzle.com/Fairdice.htm
- [7] International Bone Rollers’ Guild, Mitchel D Klink http://web.archive.org/web/20071118155413/http://members.aol.com/dicetalk/ (was http://members.aol.com/dicetalk/polymore.htm )
- [8] Polygon Names: http://www.math.com/tables/geometry/polygons.htm
- [9] Isohedra (loki3): http://loki3.com/poly/isohedra.html
- [10] Crystallographic Polyhedra, Steffen Weber http://jcrystal.com/steffenweber/













































 Chessex
Chessex




 DiceLab
DiceLab






















































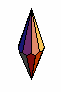





























































 tip
tip