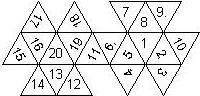
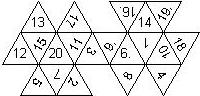
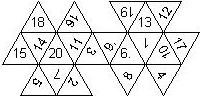
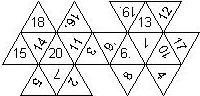
Configurations

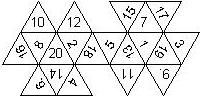
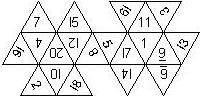
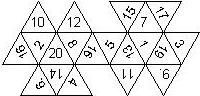
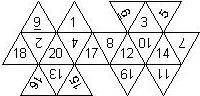
There are surprisingly many ways to put pips and numbers on a die. Here the attempt is made to describe the various configurations in a formal way. The objective was to have a unique description which allows the automatic generation of the net of a die.

For a consistent nomenclature, we have to consider both the order in which the numbers are printed on the faces as well as the orientation of each number (or constellation of pips) on a face.

Unfortunately, no consistent nomenclature has been developed yet that holds for all dice. In the sequel, different nomenclatures are used for
D4: there are two orders (called right-handed and left-handed) and two types of orientations: numbers can be put in the corners or on the edges. Of the total of four possible configurations only two so seem to exist on commercial dice.
D6: Assuming that opposite faces sum to 7, there are only two orders to put the numbers or pips on a D6. This has as already pointed out by Dennis Evans, who introduced the notation of right-handed and left-handed pipped dice.

Pipped D6: There are two different orientations each for the pips of a “2”, “3”, and “6”, yielding 16 different configurations, eight right-handed and eight left-handed ones. If the pips of the “2” are not diagonal, as in Chinese dice, there are another 16 configurations. There are other dice where the “6” (and sometimes also the “4” and “5”) are printed diagonally, and there are a few “circular” constellations.
Numbered D6: There are four different orientations for each of the six numbers (facing up, down, left, right), yielding 8192 configurations, half of them being right-handed and left-handed, respectively.
In addition, there are a few D6 whose opposite faces do not sum to 7.

D8, D10, D12, D16, D20, D24, and D30: For these dice, opposite faces do not necessarily sum to the same number (e.g. n+1 for a Dn). Hence, there are even more configurations than for a D6. These dice are all symmetric w.r.t. to a horizontal plane. If the largest number is on top, these dice can be viewed as consisting of an “upper” and a “lower” part.

The order is defined by rotating the die such that the largest number is on top, continuing counterclockwise on the “upper” half, followed by the number opposite of the “8” on the “lower” half, continuing clockwise on the “lower” half. In this way, the numbers on opposite faces are separated by n/2 digits. For most configurations, those numbers sum to n+1.
The definition of the orientation depends on the shape of the faces. For triangular faces, there are 6 possible orientations (rotated by multiples of 60°), for pentagonal faces there are 10 possible orientations (rotated by multiples of 36°)

D3, D5, D7, D14, D34, D50, D100: For these dice I have identified only a single configuration so far. They are not described in the sequel.

More details are given in the next sections.

This part of my collection was motivated by Dennis Evans’ analysis of “Coordinate Systems and Spot Nomenclature for cubic, six sided dice” and Kevin Cook’s page on “How do you tell who made a die?”. It was further stimulated when I discovered Leo van der Hejdt’s excellent book “Face to face with DICE”.

D4

The numbers on a tetrahedron can be put on the edges (base line) or in the vertices (corner). In the first case, the rolled number is at the bottom, in the second case at the top.

The numbers can be printed in two different orders on a tetrahedron, which we call left-handed and right-handed. On a right-handed (left-handed) tetrahedron, the numbers 1-2-3 and 1-3-4 are printed clockwise (counterclockwise), the numbers 1-2-4 and 2-3-4 counterclockwise (clockwise). In short, if on a face both “1” and “3” are visible, or if the sum of the numbers is odd, and the numbers are printed clockwise, then the tetrahedron is called right-handed. This holds for both the base-line and the corner version.

I haven’t found any left-handed tetrahedra yet, not even on Kevin Cook’s Megapage.

In brackets we give the nomenclature used by Kevin Cook (as indicated by the names of the figures on his home page), where available. Almost all commercially available tetrahedral use a right-handed configuration, i.e. the numbers 1-2-3 are printed clockwise (this implies that 1-3-4 are also clockwise, whereas 1-2-4 and 2-3-4 are counter-clockwise). The only exceptions I have found so far are a 50mm foam die and a 15mm porcelain die.

Base line,

right-handed

(d4_1)

Base line,

left-handed

foam, 50mm, Koplow (left)

porcelain, 15mm (right)

Corner,

right-handed

(d4_3)

Corner,

left-handed

Base line,

right-handed

Armory 1^st generation

One “1” is replaced

by an “A” (see top)

(d4_2)

pipped

AV Designs /

Shapeways

parallel inner

faces,

numbered

Magic / Shapeways

Opposite faces sum to 5

(d4_4)

Crystal Caste

Opposite faces sum to 5

Bear Cub Machine

D6

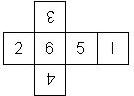
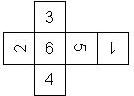
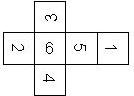
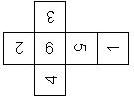
There are 30 different ways (orders) to put the numbers or pips on a D6 (irrespective of their orientation). Interestingly, out of these 30 different orders, only two “were able to struggle through a period of over two thousand years”, as Leo van der Hejdt points out in his book “Face to face with DICE”. These two are characterized in that the numbers on opposite faces sum to 7. In the next sections we assume that opposite faces of a D6 sum to 7. All possible orders are described systematically here at the end of the D6 section.

D6 Pipped

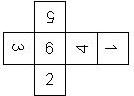
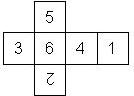
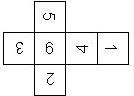
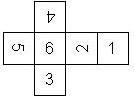
Motivated by Dennis Evans, the two possible orders are called “right handed (RH)” and “left handed (LH)”, where we assume that opposite faces sum to 7. If the “6” is on top, and the die is rotated such that both “2” and “3” are visible, the “2” can be on the right hand side (for a RH=”right handed” die) or on the left hand side (for a LH=”left handed” die).

There are sixteen different ways to put the pips on a die (orientations). How come?

The pip configurations representing “1”, “4”, and “5” are 90 degree rotation invariant. This means that when the configuration is rotated by multiples of 90 degrees, the original configuration results. This does not hold for “2”, “3”, and “6”, which are only 180 degree rotation invariant, i.e. if rotated by 90 degrees a different configuration is created. Hence, there are two ways each to put the pips of a “2”, “3”, or a “6” on the face of a die, yielding in 8 possible configurations. Considering that there are both left-handed and right-handed D6, this leads to a total of 16 possible configurations, 8 left handed and 8 right handed.

Details are described here, from where the nomenclature used in this section is taken. An earlier nomenclature (letters A..Q) was introduced by Walter Kirsch, as quoted here (“Diagonalzweier”, meaning “diagonal 2”). It is added in brackets in the pictures below.

In this section the dice are shown such that the “6” is on top and “2” and “3” are visible.

“RH000” is the name of the default configuration. If in the name a zero is replaced by a 2, 3, or a 6, this indicates that the corresponding face of the die is rotated by 90 degrees with respect to the reference configuration. The same holds for left handed dice.

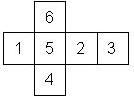
RH000 (G)

RH002 (H)

RH030 (E)

RH032 (F)

RH600 (P)

RH602 (Q)

RH630 (N)

RH632 (O)

LH000 (B)

LH002 (A)

LH030 (D)

LH032 (C)


LH600 (K)	LH602 (I)	LH630 (M)	LH632 (L)

Another complete collection can be found here.

D6 Asian Style

These are examples where the pips of the “2” are not diagonal, but horizontal or vertical, yet the numbers on opposite faces sum to 7. This seems to be a feature of Chinese dice (Japanese seem to use diagonal “2”s.). In some cases, the “1” is much larger and more deeply incised than the other spots (possibly to compensate for its opposite, the "six."), and it can be red. The pips of the “4” can also be red. Thai dice have a red “1” and “4”, and the “1” has an additional concentric circle.

“2” horizontal

“1” point-circle

“1” and “4” red

Thai

“2” vertical

“1” large

“1” and “4” red

Chinese

“2” vertical

“1” large

“1” red

“2” vertical

“1” red

“4” red

“5” center dot red

Bhutanese?

“2” horizontal / vertical

“1” normal size

Single color

“2” vertical

“1” large

Single color

“2” diagonal

“1” large

“1” and “4” red

“2” diagonal

“1” normal size

“1” and “4” red

“2” diagonal

“1” large

“1” red

“2” diagonal

“1” normal size

“1” red

“6” yellow

“2” horiziontal

“1” large

“1” and “4” red

“2” vertical

“1” large

“1” and “4” red

Blue-white striped foil

“2” diagonal

“1” large

“1”, “3” and “5” red

Opposite faces do not sum to 7

Chinese rubber die (12mm)

“2” horizontal

“1” large

Red foil

Hole on edge 6-2 (bead?)

24mm

(traded, no longer in my collection)

The origin of the custom of painting the "fours" red is accounted for, according to the a Kan san sai dzu e, by the following story (as pointed out by Merari in the Dice Maniac’s Club):

An emperor of the Ming dynasty (AD 1368-1643) played at sugoroku with his queen. He was almost defeated by her, but had one way of winning through the dice turning "fours." He cried and threw the dice, and they came as he desired, whereupon he was exceedingly glad, and ordered that the "fours" thereafter be painted red, in remembrance of his winning.

www.gamesmuseum.uwaterloo.ca/Archives/Culin/Dice1893/dice.html

In Japan, the one is large and red as in China but the four pips are normal sized and black just like western dice. One other feature that distinguishes Japanese dice from Chinese dice - the two spot is diagonal, unlike the orthogonal Chinese two-spot.

Dice from Bhutan (and Malaysia?) seem to have a large red one spot and a red four spot and in addition, the five spot has the central dot in red, while the surrounding four dots are black.

Four is an unlucky number for Chinese because it sounds the same as 'death'.

There are 16 possible configurations of these dice. The nomenclature used is similar to the one in the previous section. However, a “v” of a “h” in the position of the “2” indicates that the two pips are vertical or horizontal, respectively. Added in brackets is the nomenclature introduced by Walter Kirsch, as quoted here (“Parallelzweier”, meaning “parallel 2”).

My collection is still incomplete …


RH00v (GH1)	RH00h (GH2)	RH03v (EF1)	RH03h (EF2)


RH60v (PQ1)	RH60h (PQ2)	RH63v (NO1)	RH63h (NO2)


LH00v (AB1)	LH00h (AB2)	LH03v (CD1)	LH03h (CD2)


LH60v (IK1)	LH60h (IK2)	LH63v (LM1)	LH63h (LM2)

Other pipped D6

In addition to the “Western” and “Asian” pipped D6, there are others with different orientations of the pips. There are Russian dice where the “6” (and sometimes also the “4” and “5”) are diagonal.

There are two photos for each die. The left one shows the die with the largest number on top and the next possible largest number clockwise. The right photo shows the die when it is rotated by 180 degrees along the horizontal axis which lies in parallel to the screen. In this way, the opposite faces are shown top-top, left-right and right-left.

Russian die: “6” diagonal upright, “4” and “5” “standard”

Left handed, opposite faces sum to 7

Russian die: “6” diagonal flat

Opposite faces do not sum 7

Russian die: “6” diagonal flat

Opposite faces do not sum 7

Russian die: “6” and “5” diagonal

Opposite faces do not sum 7

“2” and “5” tilted

“4” and “5” tilted

Bought in the former German Democtratic Republic

6-1 5-4 3-2

“2” vertical, “3” tilted

“Random” pips

Right handed, opposite faces sum to 7

“Shaken” die by Atypyk

Right handed, irregular pips

Eyes Die by stop4stuff /

Shapeways

Left handed, opposite faces sum to 7

Q-Workshop, Cyber

Left handed, opposite faces sum to 7

“6” circular

Ukrainian bone die

Left handed, opposite faces sum to 7

“Circular” configuration

Configuration and pips are n-sided polygons where n is the number of pips on that face.

Exception: “1” consists of 8 arrows.

Chessex, Arrows of Chaos

Left handed, opposite faces sum to 7

“Circular” configuration

Bear Cub Machine

2 horizontal/vertical, 3 triangular, 5 pentagonal, 6 pentagonal with center pip

6-2 5-3 4-1

Reflex

2 horizontal/vertical, 3 triangular, 5 pentagonal, 6 pentagonal with center pip

6-2 5-3 1-4

Reflex

Left handed, opposite faces sum to 7

“Offset” configuration

Bear Cub Machine

Hearts

Left handed, opposite faces sum to 7

Configuration of “4” and “5” is rotated by 45 degrees

Set of 6 Asian dice with 5 blank faces each. According to Pwee Keng-Ho, these are dice for a game known as Mang Kung Sek (in Cantonese) or Zhair Mair Kow (in Hokkien), roughly meaning 'blind man's dice'.

Pips point circle or “bull’s eye”

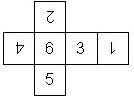
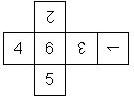
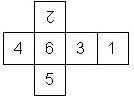
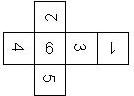
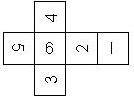
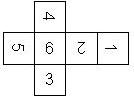
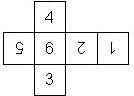
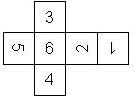
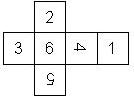
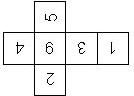
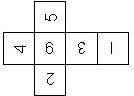
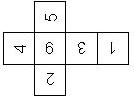
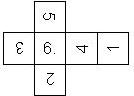
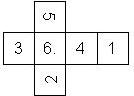
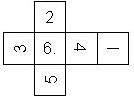
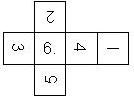
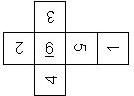
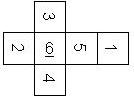
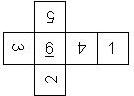
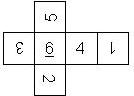
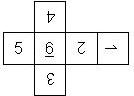
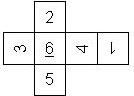
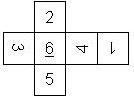
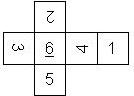
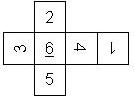
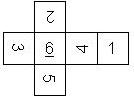
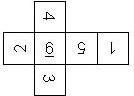
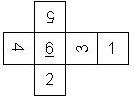
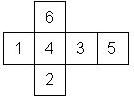
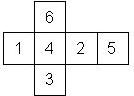
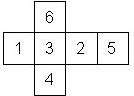
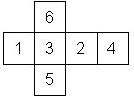
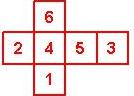
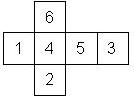
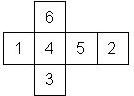
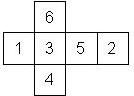
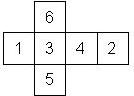
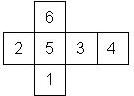
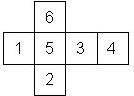
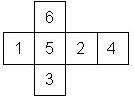
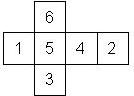
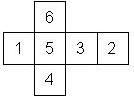
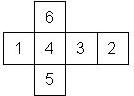
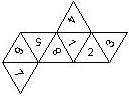
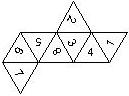
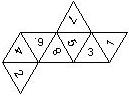
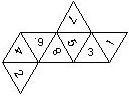
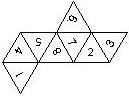
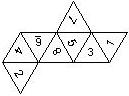
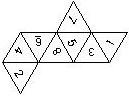
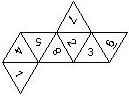
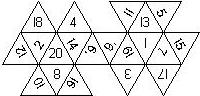
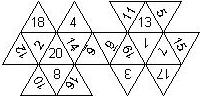
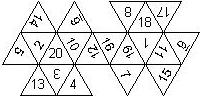
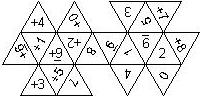
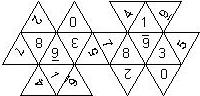
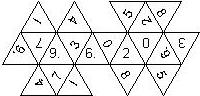
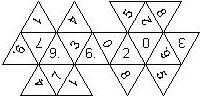
D6 Numbered

This section includes dice numbered 1..6 whose opposite faces sum to 7. There are various ways to put the 6 numbers on a die. The die can be left handed or right handed (see pipped D6), each of the six numbers can be in four different positions (facing up, down, left, right), yielding 2 x 4^6 = 8192 configurations. This number is multiplied by 9 if is distinguished if the number 6 is printed plain, underlined or dotted, and if the number 1 is printed as “1” or “I”.

In the remainder of this section there are two photos for each die. The left one shows the die such that “6” is on top and “4” and “5” are visible. The right photo shows the die when it is rotated by 180 degrees along the horizontal axis which lies in parallel to the screen. In this way, the opposite faces are shown top-top, left-right and right-left.

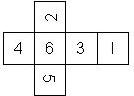
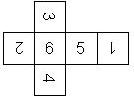
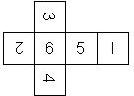
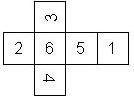
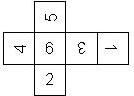
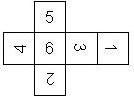
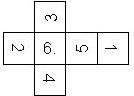
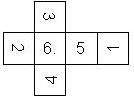
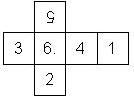
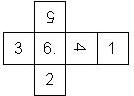
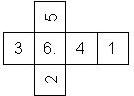
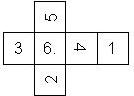
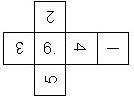
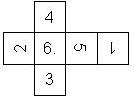
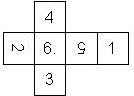
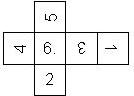
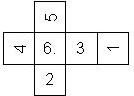
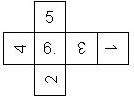
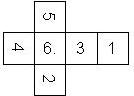
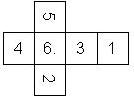
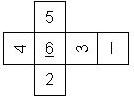
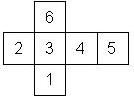
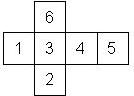
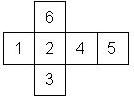
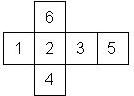
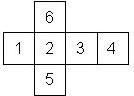
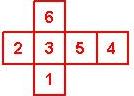
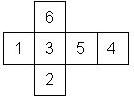
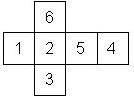
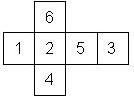
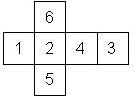
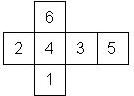
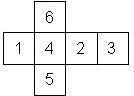
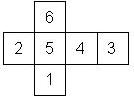
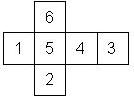
Nomenclature: In analogy to pipped D6, if the “6” is followed by the “5” in clockwise direction, the die is called right handed (RH), otherwise it is left handed (LH). The “6” and the “1” may have one of the following orientation: upper right (UR), upper left (UL), lower right (LR), lower left (LL). If the “one” is printed as “I”, we only use UR and UL. The other numbers may have one of the following orientations (clockwise): up (U), right (R), down (D), left (L). The “6” is written as 6_ (underlined), 6. (dotted), or 6 (plain). We start with RH or LH, followed by the orientation of the numbers in decreasing order.

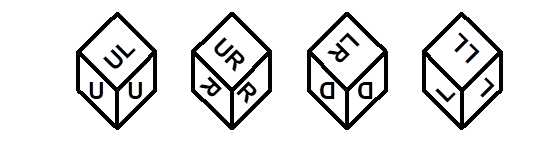
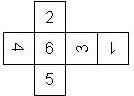
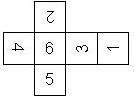
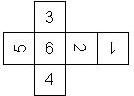
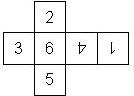
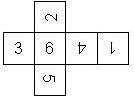
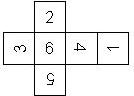
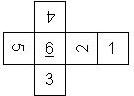
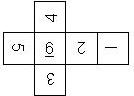
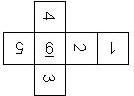
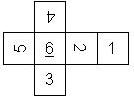
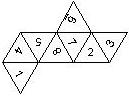
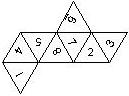
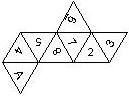
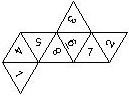
This nomenclature, albeit somewhat awkward, uniquely describes all possible numbered D6, and it can be used to automatically generate the net of a die, as shown below.

The dice are sorted as follows:

6 plain, 6 dotted, 6 underscored
RH, LH
6UL, 6UR, 6LR, 6LL
5U, 5R, 5D, 5L
4U, 4R, 4D, 4L
3U, 3R, 3D, 3L
2U, 2R, 2D, 2L
1UL, 1UR, 1LR, 1LL
1, I

In brackets we give the nomenclature used by Kevin Cook (as indicated by the names of the figures on his home page), where available.

6 Plain

RH6UL5U4U3D2U1UR (N/A)

wooden

RH6UL5U4U3D2D1LR (d6_1)

Armory 1^st generation (left), Armory Chameleons (right)

RH6UL5U4R3L2D1UR (N/A)

TV Scene It

RH6UL5U4L3R2D1LR (N/A)

wooden

RH6UL5U4L3L2D1LL (d6_9)

RH6UL5R4U3U2L1UR (N/A)

wooden

RH6UL5R4L3L2LIUR (d6_9)

TSR Dragon Dice

RH6UL5L4D3UR2RILL Gamescience (d6_6)

Note that “I” is diagonal!

RH6UR5R4R3R2L1UL (d6_3)

TSR Basic Dungeons & Dragons Original Edition

RH6UR5R4R3R2LIUL (d6_3)

Same as above, but “I” instead of “1”

Chessex Germany (left), TSR Dungeons & Dragons, 1983 (right)

RH6UR5R4R3L2R1LR (N/A)

RH6UR5R4D3D2RIUL (N/A)

Plastic, hollow, 25mm

RH6UR5D4U3U2U1UL (N/A)

wooden

RH6UR5D4R3L2D1L (N/A)

wooden

RH6UR5D4L3D2L1UR (N/A)

Same config as Chessex (d6_2), but 6 is not underlined

RH6LR5U4U3D2D1LR (N/A)

Note that the “6” is rotated by 180deg compared to the Armory 1^st generation

and Armory Chamaleons (RH6UL5U4U3D2D1LR)

Armory 2nd generation

RH6LR5D4R3R2U1UR (N/A)

GameStation Art Deco

RH6LR5L4U3L2U1LR (N/A)

Gamescience Precision Aqua

RH6LL5U4U3D2D1UL (N/A)

RH6LL5U4R3R2DIUL (N/A)

GameStation Old English

RH6LL5U4L3D2R1UR (N/A)

wooden

RH6LL5R4D3D2R1LR (N/A)

Q-Workshop Runic (left), Q-Workshop Digital (right)

LH6UL5U4U3U2D1UR (N/A)

WiR2 Die

em4miniatures

LH6UL5D4U3U2U1UR (N/A)

wooden

LH6UR5U4L3R2U1UL (N/A)

Q-Workshop Skull

LH6UR5R4L3R2L1UL (N/A)

Knights of the Dinner Table

Flying Buffalo

LH6UR5D4D3U2U1UR (N/A)

Diamond Dice

LH6UR5D4D3R2U1LR (N/A)

wooden

LH6LL5R4R3R2U1LR (N/A)

Red Jasper

Crystal Caste

LH6LL5R4D3R2UIUL (N/A)

LH6LL5R4D3R2U1LR (N/A)

Similar as above, but different font (see 1 and 3)

Porcelain, 10mm

LH6LL5R4D3R2D1UR (N/A)

Jumbo, ? (left), Koplow (right)

Same configuration but different font (see e.g. “3”)

LH6LL5D4D3U2U1UR (N/A)

GameScience Traveller Dice

6 Dotted

RH6.UR5U4R3L2D1LL (N/A)

wooden

RH6.UR5R4L3R2D1UR (N/A)

wooden

RH6.LR5U4R3R2D1UR (N/A)

RH6.LR5U4D3R2D1UR (d6_11)

Crystal Caste?

RH6.LR5R4R3R2R1UR (N/A)

RH6.LR5R4D3R2R1UR (N/A)

RH6.LR5L4U3L2U1UL (N/A)

RH6.LR5L4R3R2R1UR (N/A)

LH6.UR5L4D3U2UIUR (N/A)

LH6.UR5L4D3D2DIUR (N/A)

LH6.UR5L4D3L2DIUR (N/A)

LH6.LR5D4D3D2U1LL (N/A)

LH6.LR5L4D3D2D1UR (N/A)

LH6.LL5R4D3R2D1UR (N/A)

LH6.LL5R4D3L2D1LL (N/A)

LH6.LL5D4D3R2R1UR (N/A)

LH6.LL5L4U3L2L1UL (N/A)

LH6.LL5L4L3L2L1UL (N/A)

6 Underlined

RH6_UR5D4L3D2L1UR (d6_2)

Chessex

RH6_UR5D4R3R2D1LL (N/A)

“W. Germany”

RH6_LR5U4L3D2R1UR (N/A)

RH6_LR5R4R3L2L1LL (N/A)

RH6_LL5U4U3D2D1UL (N/A)

RH6_LL5U4R3U2RIUR Windmill (d6_7)

RH6_LL5R4L3L2U1LR (N/A)

Bakelite ?

RH6_LL5D4U3D2U1UL (N/A)

RH6_LL5L4U3U2R1UR (N/A)

LH6_UR5U4U3U2U1UL (d6_5)

LH6_UR5U4U3D2U1UL (N/A)

LH6_UR5U4U3D2D1LR (N/A)

LH6_UR5U4D3U2U1UL (d6_4)

Chessex Taiwan (top left)

Nin Gonost (bottom)

LH6_UR5R4U3D2D1LR (N/A)

LH6_LR5L4L3L2U1LL (N/A)

Bakelite ?

LH6_LL5U4U3D2D1UL (N/A)

LH6_LL5D4D3D2DIUL (d6_8)

White Wolf

Opposite faces sum to 7

(d6_10)

Crystal Caste

Opposite faces sum to 7

(N/A)

Acorn Die by Matt Bowman

D6 Orders

How many orders are there for a D6, i.e., how many different ways are there to put the numbers or pips on a D6 (irrespective of their orientation)? The answer is 30. Let us assume without loss of generality that the “6” is on top. Then there are five different numbers that can be put on the bottom, leaving four numbers on the remaining faces (denoted “a”, “b”, “c”, and “d”). Because of rotational symmetry we can further assume without loss of generality that number “a” is on the face which is facing the observer. This leaves six (3!=3·2·1=6) possibilities to put the numbers “b”, “c”, and “d” on the die. Hence, there are 5·6=30 different orders.

For the definition of the nomenclature of the order of a D6 we assume that the die is placed such that the “6” is on top and that the next highest possible number is on the right (this is the “5” unless the “5” is opposite of the “6”, in which case the next highest possible number is the “4”). We denote each configuration by pairs of opposite numbers starting with the “6”, followed by the next highest possible number and finally the third visible number, as shown below:

6-1 5-2 4-3

The next table shows all 30 possible orders of a D6. The red and blue orders are available in my collection.

6-1 5-3 4-2

6-2 5-3 4-1

6-3 5-2 4-1

6-4 5-2 3-1

6-5 4-2 3-1

6-1 5-2 3-4

6-2 5-1 3-4

6-3 5-1 4-2

6-4 5-1 2-3

6-5 4-1 2-3

6-1 5-4 3-2

6-2 5-4 3-1

6-3 5-4 2-1

6-4 5-3 2-1

6-5 4-3 2-1

6-1 5-2 4-3

6-2 5-1 4-3

6-3 5-1 4-2

6-4 5-1 3-2

6-5 4-1 3-2

6-1 5-4 2-3

6-2 5-4 1-3

6-3 5-4 1-2

6-4 5-3 1-2

6-5 4-3 1-2

6-1 5-3 2-4

6-2 5-3 1-4

6-3 5-2 1-4

6-4 5-2 1-3

6-5 4-2 1-3

Interestingly, out of these 30 different orders, only two “were able to struggle through a period of over two thousand years”, as Leo van der Hejdt points out in his book “Face to face with DICE”. These two are characterized in that the numbers on opposite faces sum to 7, and they are marked in red in the above table (6-1 5-2 4-3 and 6-1 5-2 3-4). These correspond to right-handed (RH) and left-handed (LH) dice introduced earlier: and LH correspond to the orders 6-1 5-2 4-3 and 6-1 5-2 3-4, respectively.

The pictures below show the orders of the various D6 in my collection.

6-1 5-2 4-3, “standard” RH, opposite faces sum to 7

6-1 5-2 3-4, “standard” LH, opposite faces sum to 7

6-1 5-4 3-2

“3” vertical

6-2 5-1 4-3

Top: Cheap small die, “China Rinco”

Bottom: wooden die

Pictures on the right show that 6 and 1 are adjacent

6-2 5-1 3-4

Russian die with diagonal 5 and 6

Picture on the right show that 6 and 1 are adjacent

6-2 5-3 4-1

Reflex, cicular pips (top)

Christmas Ornament (bottom)

6-2 5-3 1-4

Reflex, cicular pips

6-3 5-2 4-1

Gamescience translucent (d6_6)

Picture on the right shows that 6 and 1 are adjacent

6-3 5-2 4-1

Gamescience

Same order as above, but orientation of “1” is different

Picture on the right shows that 6 and 1 are adjacent

6-3 5-2 4-1

Las Vegas

Same order as above, but pipped

Picture on the right shows that 6 and 1 are adjacent

6-3 5-2 1-4

From the game “World of Warcraft (WoW)” (left) www.ude.com/wow

Unkown hollow pastic die (right)

6-4 5-1 3-2

12mm

6-4 5-2 3-1

12mm Chinese rubber die

(3 is misprinted)

6-4 5-2 1-3

Math expressions die

6-4 5-3 2-1

6-4 5-3 1-2

Russian die (“6” diagonal)

6-5 4-2 3-1

Top: Russian die (“6” diagonal)

Center: Chinese rubber die (12mm)

Bottom: Foggle, wood, 19mm

6-5 4-2 1-3

Pipped tablecloth weight (top, 25mm)

Unknown (2^nd row)

Tumble Numble (3^rd row left), unknown (3^rd row right)

123 Dice (bottom left) Number Please! (bottom right)

D6PN

There are a few D6 dice that come with both numbers and pips.

There is a special D6 with pips and numbers: 6,5,4,2,1 pipped, 3 numbered. It was made by Hasbro for the Monopoly Dale Earnhardt Edition (a famous US race car driver with a #3 race car)

3 numbered, 1,2,4,5,6 pipped

Hasbro

There are special D6 with 1-3 both as numbers and pips:

D6 2x(1-3)

1-3 numbered

1-3 pipped

Surprisingly, there are various configurations. In the sequel we show two pictures of those dice, the left one showing all numbers with the “3” on top and the right showing one all pips. The right photo is obtained by rotating the die by 180 degrees along the horizontal axis which lies in parallel to the screen. In this way, the opposite faces are shown top-top, left-right and right-left.

We use the following nomenclature: We start with the orientation of number “3” (UR,LR,LL,UL), continuing clockwise (2,1 or 1,2, each with U,R,D, or L), further with the pipped “3” (U for “upright” and F for “flat”; the terms “horizontal” and “diagonal” are not appropriate because the 3 is in fact diagonal), continuing counter-clockwise (2,1 or 1,2, where the “2” can be UR or UL).

3UR2D1R3F12UL


3LR1U2U3F2UL1	3LL1U2U3U12UR	3LL1D2L3U12UR


3LL1L2U3U12UL	3UL1U2U3F2UL1	3UL1D2U3U2UL1

So far there are seven different configurations in my collection.

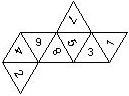
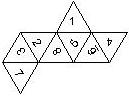
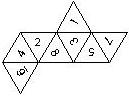
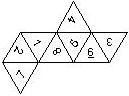
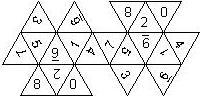
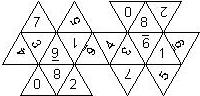
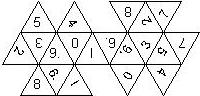
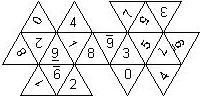
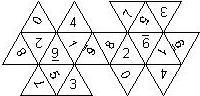
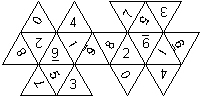
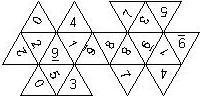
D8

In this section we consider octahedra, which we view as consisting of an “upper” and a “lower” pyramid. The “upper” pyramid is defined by the four faces that can be seen when face number 8 is on top, see photos.

For the nomenclature, we have to consider both the order in which the numbers are printed on the faces as well as the orientation of each number on a face.

The order is defined by rotating the die such that the “8” is on top, continuing counterclockwise on the “upper” pyramid, followed by the number opposite of the “8” on the “lower” pyramid, continuing clockwise on the “lower” pyramid. In this way, the numbers on opposite faces are separated by four digits. For most configurations, those numbers sum to 9.

For the orientation of the numbers on the faces, we define a default configuration where each number is printed upright (U) with respect to the baseline of the “upper” or the “lower” pyramid, respectively. By rotating the number by 60 degrees, five more configurations can be created. They are denoted as follows


U (up, default)	LR (lower right)	LL (lower left)	D (down)	UL (upper left)	UR (upper right)

Finally, we distinguish the cases where the “6” is plain, underlined (6_), or dotted (6.), and the “1” is printed as “1” or “I”.

This nomenclature uniquely describes all possible numbered D8, and it can be used to automatically generate the net of a die, as shown below.

In brackets we give the nomenclature used by Kevin Cook (as indicated by the names of the figures on his home page), where available.

6 Plain

8U6U4U2U1U3U5U7U

(d8_4, but 6 is plain)

opposite faces sum to 9

Koplow Jumbo

8U5U6U7U3U2U1U4U

(N/A)

TSR, Battle Box

8U5U6U7U1U4U3U2U

(d8_10)

Opposite faces sum to 9

Q-Workshop, Skull

6 Dotted

8U6.U4U2U1U3U5U7U

(d8_4, not shown if 1 or I)

opposite faces sum to 9

plastic (left), porcelain (right, “1” with serifs)

8U6.U4U2UIU3U5U7U

(d8_4, not shown if 1 or I)

opposite faces sum to 9

same as above, but “I” instead of “1”

8U5U4UIU3U2U7U6.U (d8_8)

Opposite faces sum to 7 or 11

6 Underlined

8U6_U4U2U1U3U5U7U

(could be d8_2, orientation of 3 not shown)

opposite faces sum to 9

Chessex (left), TSR Basic Dungeons & Dragons Original Edition (right)

8U6_U4U2UIU3D5U7U

(could be d8_2, orientation of 3 not shown)

5 and 7 slightly tilted

opposite faces sum to 9

8U5U4U1U6_U3U2U7U (d8_3)

Unknown (left), Armory Chameleons (right)

8U5U4U1U3U2U7U6_U (d8_8)

Opposite faces sum to 7 or 11

Same as above, but lower half is rotated by 90°

Different fonts (see “3”, “1”)

Unknown (left), Unknown (center), Armory 2^nd generation (right)

8U5U4UIU3U2U7U6_U (d8_8)

Opposite faces sum to 7 or 11

Same as above, but “I” instead of “1”.

8U5U4UAU3U2U7U6_U (d8_8)

Opposite faces sum to 7 or 11

Same as above, but “A” instead of “1”

The Armory 1st generation

8U5U4U1U2U7U6_U3U (N/A)

Same as above, but lower half is rotated yet another 90°

The Armory 2^nd generation?

8U2LL3LR7U4LL6_LL5LL1LL (N/A)

Base “square” is slightly rhombic

GameScience Jumbo

8D2D4D6_D7D5D3DID (d8_9, “6” should be upside down)

Numbers are “upside down” compared to most other D8

This is not an octahedron, but a dipyramid

(triangles are iscosceles but not equilateral)

TSR Dragon Dice

8U1LL2U7LL3LL6_U5LL4U (d8_1)

Opposite faces sum to 7 or 11

Gamescience Precision Aqua

D8 8UILL2U7LL3LL6_U5LL4U (d8_1)

Same as above, but “I” instead of “1”

Windmill

Opposite faces do not sum to 9

(d8_12)

Crystal Caste

A note on Kevin Cook's page:

v d8_2 (Chessex England, Chessex Denmark, etc) does not show the orientation of the “3” (there are two different orientations in my collection, see above)

D10

In this section we consider D10, which we view as consisting of an “upper” and a “lower” half. The “upper” half is defined by the five faces that can be seen when face number 9 is on top, see photos.

We list the numbers by starting with “9”, continuing counterclockwise on the “upper” half, followed by the number opposite of the “9” on the “lower” half, continuing clockwise on the “lower” half. In this way, the numbers on opposite faces are separated by five digits. For most configurations, those numbers sum to 9.

The orientation of the numbers of all D10 in my collection is default (i.e., they are printed upright with respect to the baseline of the “upper” or the “lower” pyramid, respectively). Therefore, the “U” is skipped in the nomenclature.

In brackets we give the nomenclature used by Kevin Cook (as indicated by the names of the figures on his home page), where available.

I0U6.U4U8U2UIU5U7U3U9.U (N/A)

Numbers 1-10

Even numbers on upper half, odd numbers on lower half

Opposite faces sum to 11

10U2U8U4U6.U1U9.U3U7U5U (N/A)

Numbers 1-10, dotted

Even numbers on upper half, odd numbers on lower half

Opposite faces sum to 11

Koplow

10U2U8U4U6_U1U9_U3U7U5U (N/A)

Numbers 1-10, underlined

Even numbers on upper half, odd numbers on lower half

Opposite faces sum to 11

9_U5U6U_7U8U3U2U1U0U4U (N/A)

0..4 on lower half (increasing clockwise),

5..9 on upper half (increasing clockwise)

“World of Warcraft (WoW)”

9_U3U7U5U1U2U8U4U6_U0U (N/A)

Odd numbers on upper half, even numbers on lower half

Opposite faces sum to 11 or 1 (or always11 if 0 counts as 10)

6, 9 underlined

9_DID7D3D5D6_U4U0U8U2U (d10_3)

Even numbers on upper half, odd numbers on lower half.

Note that odd numbers are upside-down

(compared to all other D10s in my collection)

TSR Dragon Dice

9U1U7U3U5U0U8U2U6U4U (d10_1)

Odd numbers on upper half, even numbers on lower half

Opposite faces sum to 9

6, 9 plain

9.UIU7U3U5U0U8U2U6.U4U (d10_1)

Odd numbers on upper half, even numbers on lower half

Opposite faces sum to 9

6, 9 dotted

9.U1U7U3U5U0U8U2U6.U4U (d10_1)

Odd numbers on upper half, even numbers on lower half

Opposite faces sum to 9

6, 9 dotted

Same as above, but “1” instead of “I”

9_U1U7U3U5U0U8U2U6_U4U (d10_1)

Odd numbers on upper half, even numbers on lower half

Opposite faces sum to 9

6, 9 Underlined

Chessex (top, all vertices normal)

Gamescience (center, center vertices blunt)

The Armory (bottom, top and bottom vertices blunt)

9_UIU7U3U5U0U8U2U6_U4U (d10_1)

Odd numbers on upper half, even numbers on lower half

Opposite faces sum to 9

6, 9 underlined

Similar to above, but “I” instead of “1”

Koplow (left), Unknown (right, note the “dashed 7”)

9_U1U5U3U7U4U2U8U6_U0U (d10_5)

Odd numbers on upper half, even numbers on lower half

Opposite faces do not sum to 9

Diamond Dice

9U1U3U5U7U2U0U8U6U4U (N/A)

Odd numbers on upper half (increasing counterclockwise),

even numbers on lower half (increasing counterclockwise)

Opposite faces sum to 11 or 1 (or always11 if 0 counts as 10)

Q-Workshop Flaming (left) Skull (right)

Decagonal Edged Cigar

GRIDIRON MASTER / PHI SPORTS

Opposite faces sum to 11 or 1 (or always11 if 0 counts as 10)

Modified 5-antiprism (d10_4)

Crystal Caste

Opposite faces sum to 10

Modified prism

Bear Cub Machine

Opposite faces sum to 9

Truncated octahedron

Opposite faces do not sum to 9

Truncated octahedron

Oddities

10,9,...2,Ankh

Even numbers on upper half,

odd numbers on lower half

“1” replaced by an Ankh symbol

10,9,...2,rose

Even numbers on upper half,

odd numbers on lower half

“1” replaced by a rose

9U1U3U5U7UYU8U6U4U2U (N/A)

Odd numbers on upper half (increasing counterclockwise),

even numbers on lower half (increasing counterclockwise)

Opposite faces sum to 9

“0” replaced by a Yin Yang symbol

Q-Workshop Yin Yang

9_UIU7U3U5U0U8U2U6_U4U

“0” replaced by a symbol (devil?)

1,2, and 3 different color

“World of Warcraft (WoW)”

(traded, no longer in my collection)

9.UIU7U3U5U0U8U2U6.U4U

8, 9, and 0 in different color,

meaning success in

World of Darkness

(traded, no longer in my collection)

9_UIU7U3U5U0U8U2U6_U4U

8, 9, and 0 in different color,

meaning success in

World of Darkness

(traded, no longer in my collection)

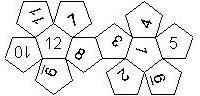
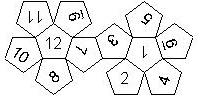
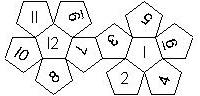
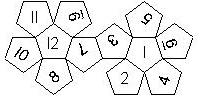
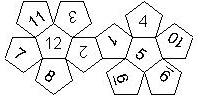
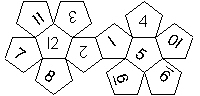
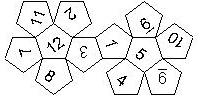
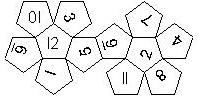
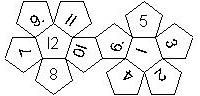
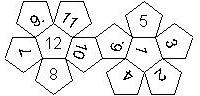
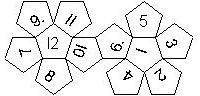
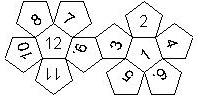
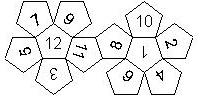
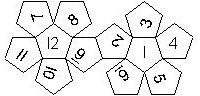
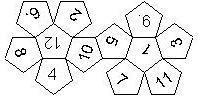
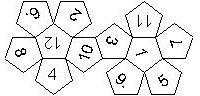
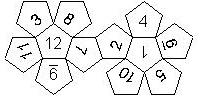
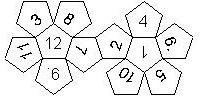
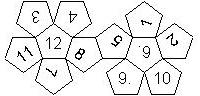
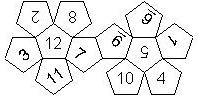
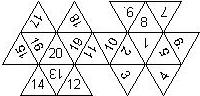
D12

In this section we consider dodecahedra, which we view as consisting of an “upper” and a “lower” half. The “upper” half is defined by the six faces that can be seen when face number 12 is on top. We assume that the “12” is upright, see photos (In rare cases, it is facing down, see e.g. here).

We define a default configuration where each number is printed upright with respect to the top or bottom pentagon, respectively. By rotating the number by multiples of 36 degrees, a total of 10 configurations can be created. They are denoted as follows

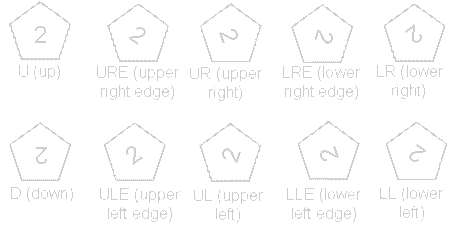
We assume that the top of the number is pointing towards a corner of the pentagon, otherwise an “E” is added (for “pointing towards the edge”).

We list the numbers by starting with “12”, continuing in the upper left counterclockwise on the “upper” half, followed by the number opposite of the “12” on the “lower” half, continuing clockwise on the upper right on the “lower” half. In this way, the numbers on opposite faces are separated by six digits. For most configurations, those numbers sum to 13.

This nomenclature uniquely describes all possible numbered D12, and it can be used to automatically generate the net of a die, as shown below.

In brackets we give the nomenclature used by Kevin Cook (as indicated by the names of the figures on his home page.

12U11UL10UL9_UL8UL7UL1UL2UL3UL4UL5UL6_UL

(N/A)

Spin-Down configuration

1..6 on lower half, 7..12 on upper half

Opposite faces sum to 13

12U11LL10LR8LR7U9_LL1U2LR3LL5LL6_U4LR

(d12_7)

1..6 on lower half, 7..12 on upper half

Opposite faces sum to 13

TSR Basic Dungeons & Dragons Original Edition

I2UIILLI0LR8LR7U9_LLIU2LR3LL5LL6_U4LR

(d12_7)

Same as above, but “I” instead of “1”

1..6 on lower half, 7..12 on upper half

Opposite faces sum to 13

“I2” slightly tilted

TSR Dungeons & Dragons, 1983

I2UIILLI0LR8LR7URE9_LLIU2LR3LL5LL6_U4LR

(d12_7)

1..6 on lower half, 7..12 on upper half

Opposite faces sum to 13

Same as above, but “I” instead of “1”

Chessex Germany

12U11U7LR8LL2UR3LR5LL6_LL1LL4U10LR9_UR (d12_1)

If 1 or 7 are on top, 2..6 and 8..12 are increasing clockwise

12U11U7LR8LL2UR3LR5LL6_LL1LL4U10LR9_UR (d12_1)

Same as above, font with serifs

12U11U7LR8LL2UR3LR5LL6_LL1LL4U10LR9_UR (d12_1)

Same as above with sharp edges

GameScience Precision (left), unknown (right, 16.4mm)

I2UIIU7LR8LL2UR3LR5LL6_LLILL4UI0LR9_UR (d12_1)

Same as above with “I” instead of “1”

Windmill

12ULE11ULE7U8LL3UR2LRE5LL4D1LR6_ULE10LR9_URE (d12_6)

If 1 or 7 are on top, 2..6 are increasing counterclockwise,

8..12 are increasing clockwise.

Numbers not centered / aligned

GameScience Jumbo

I2UI0LL6_LLIUL5LR3URE2LREIILR9_LR7LL4LR8U (d12_9)

Opposite faces do not sum to 13

TSR Dragon Dice

I2U9.U7U8UI0UIIUIUL4U6.U5U3U2U (d12_8)

1..6 on lower half, 7..12 on upper half

Opposite faces sum to 13

12U9.U7U8U10U11U1UL4U6.U5U3U2U (d12_8)

1..6 on lower half, 7..12 on upper half

Opposite faces sum to 13

Same as above, but “1” instead of “I”

I2U9.U7U8LLI0UIIUIUL4U6.U5U3U2U (N/A)

1..6 on lower half, 7..12 on upper half

Opposite faces sum to 13

Same as above, but ‘8’ has different orientation

Crystal Caste Brass 12mm

12U8U10U11U9.U7U1LR5U3U2U4U6.U (N/A)

1..6 on lower half, 7..12 on upper half

Opposite faces sum to 13

12U7U5U3U11U9U1U6U8U10U2U4U (N/A)

Opposite faces sum to 13

Q-Workshop, Skull

I2U7ULIILRI0UL9_UL8ULIU6_UL2UL3UL4UL5UL (N/A)

1..6 on lower half (increasing clockwise),

7..12 on upper half (increasing clockwise)

Opposite faces sum to 13

12D6.D8D4D10D2D1URE7D5D9.D3D11D (d12_11, but lower half is not shown)

Even numbers on top, odd at bottom

Opposite faces sum to 13

12D6.D8D4D10D2D1LLE9.D3D11D7D5D (d12_11, but lower half is not shown)

Even numbers on top, odd at bottom

Upper half is same as above, but lower half is rotated by 144 degrees

12U3U11U9_U7U8U1U10U2U4U6_U5U (d12_3)

Opposite faces sum to 13

12U3U11U9.U7U8U1U10U2U4U6.U5U (d12_10)

Opposite faces sum to 13

Same as above, but 6/9 dotted

12U3LL11UR7UL8UL4LR6.U9.LR5UL1UL2UR10LL (d12_13)

If 1 or 7 are on top, 2..6 and 8..12 are increasing clockwise

Koplow AstroDice (20mm)

12U2LL3UR11LR7UL8LR5U10LR9_UL6_LL1UR4LL (d12_2)

If 1 or 7 are on top, 2..6 and 8..12 are increasing clockwise

The Armory

Rhombic Dodecahedron

AskAstro (left), Justin Michell (right)

Opposite faces sum to 13

(d12_12)

Crystal Caste

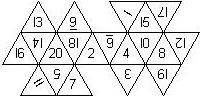
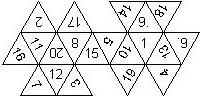
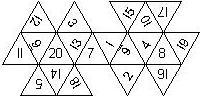
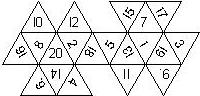
D16

In this section we consider dipyramidal D16, which we view as consisting of an “upper” and a “lower” pyramid.

We list the numbers by starting with “16”, continuing counterclockwise on the “upper” pyramid, followed by the number opposite of the “16” on the “lower” pyramid, continuing clockwise on the “lower” pyramid. In this way, the numbers on opposite faces are separated by eight digits. For most configurations, those numbers sum to 17.

There is no corresponding page by Kevin Cook.

16U2U14U4U12U6_U10U8U1U15U3U13U5U11U7U9_U

Opposite faces sum to 16

Sharp edges

6, 9 underlined

Chessex

I6U6.UI0U2UI4U8UI2U4UIUIIU7UI5U3U9.U5UI3U

Opposite faces sum to 16

Rounded edges

6, 9 dotted

Chessex

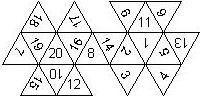
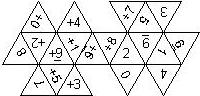
D20

In this section we consider icosahedra which we view as consisting of an “upper” and a “lower” half. The “upper” half is defined by the ten faces that can be seen when face number 20 is on top. We assume that the base of the triangle with number 20 is at the bottom, such that the “20” can face up or down, see photos. For those dice that are numbered 0..9 twice, we assume that the ‘+9’ is on top (if there is a ‘+9’), otherwise the ‘9’ with the higher number directly to its left.

We define a default configuration where each number is printed upright with respect to the top or bottom triangles, respectively.


U (up, default)	LR (lower right)	LL (lower left)	D (down)	UL (upper left)	UR (upper right)

We list the numbers by starting with “20”, continuing counterclockwise with the three triangles adjacent to “20”, starting on the upper left side, then continuing counterclockwise with the set of the lower 6 triangles adjacent to those other 3 triangles, again starting on the upper left side. The same procedure is repeated on the “lower half”, this time clockwise. In this way, the numbers on opposite faces are separated by 10 digits. For most configurations, those numbers sum to 21.

This nomenclature uniquely describes all possible numbered D20, and it can be used to automatically generate the net of a die.

In brackets we give the nomenclature used by Kevin Cook (as indicated by the names of the figures on his home page).

20U19LR10U16LL18LR7LL15LL12LL8LL17LL1U2LL11U5LR3LL14LR6LR9U13LR4LR (d20_24)

Opposite faces sum to 21

Q-Workshop, Skull

20U16LR13D19LL17LR15D14LR12LL11D18LL1D5UR8U2UL4UR6.U7UR9.UL10U3UL

Opposite faces sum to 21 (d20_21)

Numbers are printed in a “circular” order from bottom to top, “spin-down”

Opposite faces sum to 21

Koplow, different fonts

20U15U7U11LL13U12LR5LL2U3U17LR1U6.LR14U10LR8LR9.U16.LL19.LL18U4LL

16 and 19 with dots (“16.”, “19.”) (d20_29)

Opposite faces sum to 21

20U14U7U11LL18U15LR5LL2U3U16LR1U6.LR13U10LR8LR9.U19LL12LL17U4LL

(d20_6)

Opposite faces do not always sum to 21!

20U14U7U11LL18U15LR5LL2U3U16.LR1U6.LR13U10LR8LR9.U19.LL12LL17U4LL

Same as above, but 16 and 19 with dots (“16.”, “19.”) (d20_6)

16 and 19 are dotted

Opposite faces do not always sum to 21!

20UI4LL5UI8LRI3UI6LRIIU7LL2LL9_UI0D4LRI5U8LL3U6_LLIUI7LRI2LRI9U

(d20_15)

Opposite faces do not sum to 21!

Single digit numbers are larger than double digit numbers

TSR Dungeons & Dragons, 1983

20D11LR12D8LR2D16D7D3LR15LL17D1D10LL9.U13LR19LR5D14D18UR6.LR4UR

20 upside down (d20_5)

Opposite faces sum to 21

20U9_LRI4UI3LLI2LRIILR5ULI8LR7LL3UR4LR6_LLI0LL8LL2LRIUI5UI7LRI9LLI6U

(d20_14)

Opposite faces do not sum to 21!

TSR Dragon Dice

20U8UI4U2UI0UI6U6.U4UI8UI2UILLI3U7UI9UIIU5UI5UI7U3U9.U

Opposite faces sum to 21

Default orientation of all numbers, except 1 (d20_13)

Note: this is the same as below (d20_4), except that “20” is rotated

by 120° counter-clockwise

Chessex

20U8U14U2U10U16U6.U4U18U12U1LL13U7U19U11U5U15U17U3U9.U

Opposite faces sum to 21

Note: this is the same as above, but with “1” instead of “I” (d20_13)

20D4LLI0UI2LR7UI6LL2DI8D8LRI5U1DI7LR11U9_LLI4U5LRI9D3DI3LL6_U (N/A)

Opposite faces sum to 21

Strange font mix: „1” with serif, „11” sans serif, „I2”..”I9” with „I” instead of „1”

Jerry Alexander

20U2U14U8U10U16U6.U4U16U12U1LL13U7U19U11U5U15U17U3U9.U (N/A)

Porcelain

20U2LL13U4LR9_U18LR16LL15LR17LL1U10U12LR3U14LL19U8LL6_LR5LL7LR11U (d20_3)

Numbers on opposite faces differ by 10

The Armory 2^nd Generation (1-20)

20U2U8UI4UI8UI2UI0UI6U6.U4UIUI9UI3U7U3U9.UIIU5UI5UI7U

Default orientation of all numbers (d20_4)

Opposite faces sum to 21

20U2U8U14U18U12U10U16U6_U4U1U19U13U7U3U9_U11U5U15U17U

Default orientation of all numbers (d20_4)

Opposite faces sum to 21

Note: this is the same as above, but with “1” instead of “I”

Chessex

20U2U3U10U14LR5LL13LR4LL12LR6_LL1U19U18U11U7LL16LR8LL17LR9_LL15LR

(d20_19)

Opposite faces sum to 21

GameScience

+9_U+2LL+5LL+1U+0LR8U7U+3LL+6_U+4U9_U2LR5LR1U0LL+8U+7U3L

(d20_18)

Numbers on opposite faces are identical (with and without ‘+’ sign)

If ‘+1’ is on top, all numbers with ‘+’ signs are in the upper half

+9_U+1U+5LR+2LR+4U+6_U+3LR7U8U+0LL9_U1U5LL2LL4U6_U3LL+7U+8U0LR

(d20_11)

Numbers on opposite faces are identical (with and without ‘+’ sign)

If ‘+1’ is on top, all numbers with ‘+’ signs are in the upper half

Compared to the die above (d20_18), the numbers with and without ‘+’ sign are interchanged

Gamescience Precision Aqua

9_U8LL1LL3LR2LR7LL4U6_U5LR0U6_U8LR1U3LL2U7LR4U9_LL5LL0U

Numbers on opposite faces are identical

(looks identical to d20_2, but the numbers not shown are different)

9.U7LL7LR3LLILR9.LL4UIU6.LL4LR0U2LR2LL6.LR8LL0LR5U8U3LR5LL (N/A)

9.U7LL7LR3LL1LR9.LL4U1U6.LL4LR0U2LR2LL6.LR8LL0LR5U8U3LR5LL (N/A)

Same as above but “1” instead of “I”

9_U5LR2U1LL3LR7U8LR0LL4U6_LL9_U5LL2U1LR3LL7U8LL0LR4U6_LR (d20_2)

Numbers on opposite faces are identical

On some dice, numbers on upper half are inked, those on lower half are not

The Armory 2^nd generation (2 x 0..9)

9_U3LR8U1LR7U4U0LR2LL6_U5LL9_U3LL8U1LR7U4U0LL2LR6_U5LR (d20_10)

Numbers on opposite faces are identical

TSR Basic Dungeons & Dragons (Original Edition)

9.U3LL6.LL0LR5U2LL8LRILRILL4UR3LR9.LL2LL5U0LR6.LL8LL7LL7LR4UL

Numbering scheme is identical independently which ‘9’ is on top (d20_9)

‘4’ is not ‘sitting’ on an edge of the triangle, but on a corner

Koplow

9_U2LL9_U1U0LR8U1U2LL8LL4U5LR3LR5LR7U0U6_LL7U3LR6_U4LR

If the die were cut in half between the two 9’s, the two halves would be identical (N/A)

B&J

9_U2LL5LL1U0LR8U7U3LL6_U4U9_U2LR5LR1U0LL8U7U3LR6_U4U (d20_1)

Numbers on opposite faces are identical.

Same numbering scheme as d20_11, without ‘+’ signs

Same configuration but different fonts (see e.g. 3, 4)

GameScience (left) GameScience mini (center, 12.5mm), B&J (right)

9_U2LL5LL1U0LR8U7U3LL6_U4U9_U2LR5LR1U0LL8U7U3LR6_U4U (d20_1)

Numbers on opposite faces are identical.

Same as above with “I” instead of “1”

Windmill

9_U2LR5LL1U0LR2U0U3LL6_U4U6_LR8LL3LR1LR7LL8U7U5LR9_LR4U

Numbering scheme is identical independently which ‘9’ is on top (d20_8)

GameScience Jumbo

Opposite faces sum to 21

(d20_17)

Crystal Caste

Oddities

20U16LR13U19LL17LR15U14LR12LL11U18LL1U2LL8U5LR3LL10U9.LL7LR6.U4LR

(d20_16)

20 replaced by a Lotus symbol (life counter)

D24

The Tetrakis Hexahedron (D24) is one of two shapes used for D24 dice.. There are two different configurations in my collection. For simplicity, we only list the “24” and the three adjacent numbers in counterclockwise direction.

There is no corresponding page by Kevin Cook.

24U16U21U5U

D24 Tetrakis Hexahedron

GameScience

24U13U21U11U

D24 Tetrakis Hexahedron

The Deltoidal Icositetrahedron (D24) is the other D24 shape. It comes in two variants, the D24 by Franck Dutrain and the D-Total designed by Alexander Simkin and manufactured by Lou Zocchi’s GameScience. The latter is a true marvel, details can be found here

D24 Deltoidal Icositetrahedron

Franck Dutrain (left), A. Simkin / GameScience (right)

D30

In this section we consider Rhombic Triacontahedron (D30). There are two different configurations in my collection. For simplicity, we only list the “30” and the four adjacent numbers in counterclockwise direction, starting at top left.

In brackets we give the nomenclature used by Kevin Cook (as indicated by the names of the figures on his home page).