Spherical Dice
Spheres
Spheres with an internal Cavity and a weight
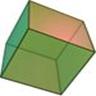
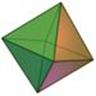
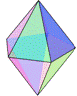
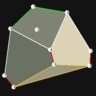
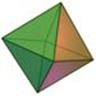
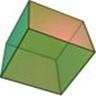
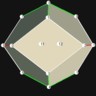
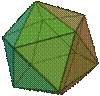
There are spherical dice with an internal cavity and a weight. When the die is rolled, the weight moves, which causes the die to settle in one of n orientations. For fair dice, the weight is a sphere itself, and the internal cavity of a spherical Dn is a often a platonic solid with n vertices (not faces!), which is also a platonic solid.
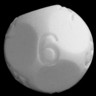
D6
|
Plastic
Wood |
|
Internal cavity ressembles an octahedron, the dual of the cube |
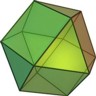
D8
|
Clsn / Shapeways |
|
Internal cavity is a cube, the dual of the octahedron. |
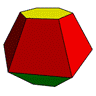
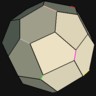
D12
|
Clsn / Shapeways |
|
Internal cavity is an icosahedron, the dual of the dodecahedron. |
Truncated / flattened spheres
Truncated or flattened spherical dice are made of spheres where n spherical caps of equal size are removed. This results in a sphere with n equal non-overlapping circles. This can also be seen as the intersection of a special n-sided polyhedron and a sphere.
When the die is rolled, it most likely stops on one of the circles. Because it might also stop on a curved part of the surface, such dice are not exactly fair in the mathematical sense, but if the circles are placed in a special manner (see below), these dice can be considered fair in a practical sense.
There are different approaches to design the intersecting polyhedron, as described by the following (not necessarily mutually exclusive) criteria:
The intersecting polyhedron is a platonic
solid. This results in “fair” dice.
The intersecting polyhedron is an isohedron
(note that platonic solids are a subset of isohedra). This results in “fair”
dice.
The intersecting polyhedron is a symmetrical
construction such that the centers of the faces are
located at the poles of the sphere and on circles parallel to the equator.
Then, the resulting polyhedron has some rotational symmetry around the axis
between the poles.
An alternative view is to place the centers of n equal non-overlapping circles according to the following (not necessarily mutually exclusive) criteria of distributing points on a sphere or packing circles on a sphere:
Packing: maximize
the minimum distance between any pair of points: This maximum distance is
called the covering radius, and the configuration is called a spherical code
(or spherical packing). Packings are the same if some orthogonal matrix
transforms one to the other.
The resulting circles that are locked into position by their neighbours are
called rigid, those are free to “move” in the small space between them and
their nearest neighbours are called rattlers.
The problem of spherical packing is sometimes known as the or Tammes problem. There
are exact solutions for 4, 6, and 12, but the general problem has not been
solved. Best known solutions are available here.
Antipodal Packing: maximize the minimum distance between any pair of points with the
constraint that there are antipodal pairs of points. This constraint leads to
parallel faces of the dice, making it possible to print the number on the
faces. Except for n=6 and n=12, the optimum solutions of the
Tammes problem (see above) are not antipodal, i.e., the resulting dice do not
have parallel faces. No systematic approach was found in the literature for
this problem. Here we try to construct optimum dice and back the results up by
brute force search methods.
Potential:
minimize the potential energy of the points: Sum 1 / dist(P_i, P_j ),
minimal 1/r potential. This is also known as Thomson problem. Best
known solutions are available here.
Check this page to display optimum truncated
spheres.
The table below shows a collection of truncated spherical dice. Full size pictures are from my own collection. Half-size pictures are from dice not (yet) in collection, picture sources are indicated in [Ref].
Symmetry is categorized according Wikipedia pages Point groups in three dimensions, Schoenflies notation and List of spherical symmetry groups.
The description was obtained from this blog or through private communication with the designers.
|
# circles, symmetry type |
Picture and Designer |
Polyhedron |
Description |
D2 / D∞h“Coin” Optimum 2-fold |
Sylook / Shapeways
McTrivia / Shapeways Missing |
Equator 2
Equator 1
Pole (2-fold) |
Intersection of two parallel planes and a sphere. “Fair”.
Optimum in the sense of “antipodal packing”. This can be seen by construction: the maximum angle between any two points on a sphere is 180°.
Parallel faces.
Phi=180°=360°/2
Symmetry type D∞h |
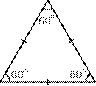
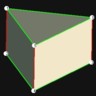
D3 / D3h“Elongated 3-Prism” Optimum 3-fold |
Magic / Shapeways
McTrivia / Shapeways Missing |
Intersecting polyhedron
Constellation
Pole (3-fold)
Equator
|
Intersection of an elongated 3-prism (“Toblerone”) and a sphere. The 3 points form an equilateral triangle. “Fair”.
Phi=120°=360°/3
Symmetry type D3h (3-fold prismatic symmetry)
No parallel faces, numbers are on the spherical part.
|
D4 / Td“Tetrahedron” Optimum
|
Magic / Shapeways
McTrivia / Shapeways Missing |
Intersecting polyhedron
Constellation (dual) |
Intersection of a
tetrahedron and a sphere. The four points form
a tetrahedron (dual). “Fair”. Optimum in the sense of “packing” and “potential”.
Phi= 109.4712206°. tan(phi/2)=sqrt(2).
Symmetry type Td (full tetrahedral symmetry).
No parallel faces, numbers are on the spherical part.
Upper die is numbered 1..4, lower 2,3,3,4 (same as 2 D2) |
D4 / C4“Elongated 4-Prism” 4-fold |
Sylook / Shapeways |
Intersecting polyhedron
Constellation
Pole (4-fold)
Equator
|
Intersection of an elongated 4-prism and a sphere. The four points form a square “Fair”.
Phi=90°=360°/4
Symmetry type C4 (4-fold rotational symmetry)
Optimum in the sense of “antipodal packing”. This can be seen by construction: two pairs of antipodal points on a sphere lie in a plane. The angle is maximized if they lie on a great circle, leading to a maximum angle of 360°/4=90°. |
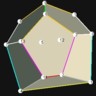
D5 / D3h“Prism” Optimum 3-fold |
Magic / Shapeways
McTrivia / Shapeways Missing |
Intersecting polyhedron
Constellation (dual)
Pole (3-fold)
Equator |
Intersection of a 3-prism and a sphere. The 5 points form a 3-bipyramid. “Fair”.
Phi= 90° (same as for D6).
3-fold rotational symmetry, 1+3+1.
Symmetry type D3h (3-fold prismatic symmetry)
Only 2 parallel faces, 3 numbers are on the spherical part
There is an infinite number of optima in the sense of “packing”. Starting with a cube with one of the equatorial circles removed, the 3 circles on the equator can be moved freely. Placing these 3 circles such that their centers form an equilateral triangle yields the 3-prism. |
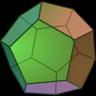
D6 / Oh“Cube” Optimum
|
Magic / Shapeways
Bo-Jo dice
Sylook / Shapeways Missing |
Intersecting polyhedron
Constellation (dual)
Pole (4-fold)
Equator |
Intersection of a sphere and a cube. The 6 points form a regular octahedron. “Fair”.
Optimum in the sense of “packing”, “potential”, and “antipodal packing”.
Parallel faces.
Phi= 90°=360°/4.
Symmetry type Oh (full octahedral symmetry).
The circles of the Bo-Jo die do not touch.
|
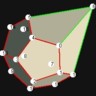
D7 / D5h“Prism” 5-fold |
McTrivia / Shapeways |
Intersecting polyhedron
Constellation (dual)
Pole (5-fold)
Equator |
Intersection of a 5-prism and a sphere. The 7 points form a 5-bipyramid. “Fair”.
Phi= 72°=360°/5
Symmetry type D5h (5-fold prismatic symmetry)
|
D7 / C2v2-fold |
Magic / Shapeways |
Intersecting polyhedron
North Pole (2-fold)
Equator
South Pole |
Symmetrical construction with 2-fold rotational symmetry, 1+4+2 (1 rhombus, 4 quads, 2 triangles).
Phi=77.25°.
Symmetry type C2v=D1h (reflection in a plane and a 180° rotation through a line in that plane)
Tranformation of a cube, where one face is cut into two in diagonal. Then, the vertices were moved to maximize the radii of the circles. Nevertheless, this is not optimum in the sense of packing. |
D7 / C3vOptimum 3-fold |
Magic /
Magic / Shapeways |
Intersecting polyhedron
North Pole (3-fold)
Equator
South Pole |
Optimum in the sense of “packing”.
Phi=77.869542°. No parallel faces.
3-fold rotational symmetry, 1+3+3 (1 equilateral triangle + 3 irregular pentagons + 3 deltoids).
Symmetry type C3v (3-fold pyramidal symmetry)
|
D8 / Oh“Octahedron” 4-fold |
Magic / Shapeways
Sylook / Shapeways Missing
LOGICAL LEARNING LTD
McTrivia / Shapeways Missing |
Intersecting polyhedron
Constellation (dual)
Pole (4-fold)
Equator
|
Intersection of an octahedron and a sphere. The 8 points form a cube. “Fair”.
Parallel faces.
Phi= 70.528779°. sin(phi/2)= 1/sqrt(3).
Symmetry type Oh (full octahedral symmetry)
Note that although the octahedron is a platonic solid, this shape is not optimum in the sense of “packing” (but the intersection of a tetragonal trapezohedron and sphere is).
Optimum in the sense of “antipodal packing”. This can be seen by construction:
From top: numbered (2x), pipped (2-9), moon phases |
D8 / D4d“4-Trapezohedron” Optimum 4-fold |
Magic / Shapeways |
Intersecting polyhedron
Constellation (dual)
Pole (4-fold)
Equator |
Intersection of a tetragonal trapezohedron and a sphere. The 8 points form a square antiprism. “Fair”.
Optimum in the sense of “packing”.
No parallel faces.
Phi= 74.8584922°.
Symmetry type D4d (4-fold antiprismatic symmetry)
|
D9 / D3hOptimum 3-fold |
Magic / Shapeways
Clsn / Shapeways
McTrivia / Shapeways |
Pole (3-fold)
Equator |
Optimum in the sense of “packing”,
Phi=70.528779°= sin(phi/2)= 1/sqrt(3). Note that this is the same angle as for the octahedron. Explanation?
3-fold rotational symmetry, 3+3+3 (3 rhombi, 6 irregular pentagons).
Symmetry type D3h (3-fold prismatic symmetry)
Magic: 1,5,9 on equator Clsn: 3,5,6 on equator McTrivia: 2,3,5 on equator
Magic’s die is numbered from 1 to 9: 6 numbers are on vertices, 3 on edges, none on the faces. The sum of the numbers on the upper vertices is 15. Same thing for the sum of the 3 numbers on the lower vertices and the sum of the 3 numbers on the edges. This numbering is closely linked to the well known 3x3 magic square.
McTrivia’s die is numbered to get the same results as throwing 2 D3s (6,5,5,4,4,4,3,3,2) |
D10 / D5d“5-Trapezohedron” 5-fold |
Magic / Shapeways |
Intersecting polyhedron
Constellation (dual)
Pole (5-fold)
Equator |
Intersection of a 5-trapezohedron and a sphere. The 10 faces are parallel to those of a dodecahedron, whose top and bottom faces are removed. The 10 points form a 5-antiprism. “Fair”.
Parallel faces.
Phi 63.44° = acos(1/sqrt(5))
5-fold rotational symmetry.
Symmetry type D5d (5-fold antiprismatic symmetry)
Optimum in the sense of “antipodal packing”. This can be seen by construction:
Numbered 0..9, also available in 00..99. |
D10 / D4h“Square bifrustum” 4-fold |
No design available yet |
Intersecting polyhedron
Constellation (dual)
|
Intersection of a square bifrustum and a sphere. The 10 faces are parallel to those of a dodecahedron, whose top and bottom faces are removed. The 10 points form an elongated square bipyramid.
The design can be described as 1+4+4+1. The maximum angle can be achieved if the triangles are equilateral, yielding phi=60°.
4-fold rotational symmetry.
Symmetry type D4h (4-fold prismatic symmetry)
|
D10 / C3v“Cuboctahedron” 3-fold |
Magic / Shapeways |
Pole(3-fold)
Equator
|
Based on a D14 (non-regular Cuboctahedron), with 4 spherical caps added to "cancel" 4 out of the 14 faces.
Phi=54.74° = arccos(1/sqrt(3)).
3-fold rotational symmetry, 1+3+3+3.
Symmetry type C3v (3-fold pyramidal symmetry)
Numbered from 0 to 9. |
D10 / D4d4-fold |
Magic / Shapeways |
Pole (4-fold)
Equator |
Symmetrical construction with 4-fold rotational symmetry. The dual polyhedron has 2 squares and 8 irregular pentagons, with the maximized radii.
Phi=65.53°.
4-fold rotational symmetry, 1+4+4+1.
Symmetry type D4d (4-fold antiprismatic symmetry)
Numbered from 0 to 9. 2 parallel faces. |
D10 / C2vOptimum 2-fold |
No design available yet |
|
Optimum in the sense of “packing.
Phi= 66.146822°.
Symmetry type C2v=D1h (reflection in a plane and a 180° rotation through a line in that plane)
2-fold rotational symmetry, 2+4+2+2. Polyhedron with 2+4 quads and 2+2 pentagons, |
D11 / C2v2-fold |
McTrivia / Shapeways |
North Pole (2-fold)
Equator
South Pole |
2-fold rotational symmetry, 2+4+4+1.
Symmetry type C2v (2-fold pyramidal symmetry)
|
D11 / unk3-fold |
|
Pole (3-fold)
Equator
Polyhedron? |
Symmetrical construction with 3-fold rotational symmetry: 1+3+3+3+1
Phi=60°=360°/6.
Symmetry type ???
Numbered such that the sum of the numbers on each of the 3 horizontal planes is 18. |
D11 / C5vOptimum 5-fold |
Magic / Shapeways
|
North Pole (5-fold)
Equator
South Pole
|
Intersection of a dodecahedron and a sphere, with 1 spherical caps added to the dodecahedron to "cancel" 1 out of the 12 faces.
Optimum in the sense of “packing”. However, the center of gravity is not at the center of the circle à not fair.
Phi 63.44° = arccos(1/sqrt(5)), same as Pentagonal Dodecahedron.
5-fold rotational symmetry, 1+5+5.
Symmetry type C5v (5-fold pyramidal symmetry) |
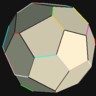
D12 / Ih“Pentagonal Dodecahedron” Optimum
|
Magic / Shapeways
|
Intersecting polyhedron
Constellation (dual)
Pole (5-fold)
Equator |
Intersection of a dodecahedron and a sphere. The 12 points form a regular icosahedron. “Fair”.
Optimum in the sense of “packing” and “antipodal packing”
Parallel faces.
Phi 63.44° = arccos(1/sqrt(5))
Symmetry type Ih (full icosahedral symmetry) |
D13 / unk |
McTrivia / Shapeways |
|
Unknown design |
D13 / C4vOptimum 4-fold |
Magic / Shapeways |
North Pole (4-fold)
Equator
South Pole |
Optimum in the sense of “packing”, phi= 57.1367031°.
4-fold rotational symmetry, 1+4+4+4.
Symmetry type C4v (4-fold pyramidal symmetry)
|
D14 / OhCuboctahedron
|
Magic /
Magic / Shapeways
Card Dice
|
Pole (4-fold)
Equator
|
Intersection of a cuboctahedron and a sphere.
Phi=54.74° = arccos(1/sqrt(3)).
4-fold rotational symmetry, 1+4+4+4+1 and 3-fold rotational symmetry, 1+3+3+3+3+1.
Symmetry types Oh (full octahedral symmetry) and Td (full tetrahedral symmetry)
|
D14 / D6h“Hexagonal bifrustum” 6-fold |
No design available yet |
Intersecting polyhedron
Constellation (dual)
|
Intersection of a hexagonal bifrustum and a sphere. The 14 points form an elongated hexagonal bipyramid.
The design can be described as 1+6+6+1. The maximum angle can be achieved if the quadrangles are squares, corresponding to an angle theta of the horitontal plane of 63.435°, yielding
Phi=53.13°
Parallel faces.
6-fold rotational symmetry.
Symmetry type D6h (6-fold prismatic symmetry) |
D14 / D2dOptimum 2-fold
|
No design available yet |
|
Polyhedron consists of 4+8 pentagons and 2 hexagons
Optimum in the sense of “packing”.
Phi= 57.1367031°.
2-fold rotational symmetry, 1+4+2+2+4+1
Symmetry type D2d (2-fold antiprismatic symmetry) |
D15 / D5h5-fold |
Magic / Shapeways
|
Pole (5-fold)
Equator |
Symmetrical construction with 5-fold rotational symmetry: 5+5+5.
Phi=52.501308°.
Symmetry type D5h (5-fold prismatic symmetry)
Numbered from 1 to 15: all numbers are on edges. The sum of the numbers on each tropic is 40 and the same applies to the equator. Except for 8, all the numbers go by pair summing to 16: on the tropic two numbers symmetric relatively to the plane of the equator sum to16 and on the equator circle itself two numbers symmetric relatively to number 8 sum to 16. |
D15 / unk |
McTrivia / Shapeways |
|
Unknown design |
D15 / C1Optimum No symmetry |
No design available yet |
|
Polyhedron consists of 12 pentagons and 3 hexagons
Optimum in the sense of “packing”.
Phi= 53.6578501°.
Symmetry type C1 (no symmetry) |
D16 / D4dOptimum 4-fold |
Magic / Shapeways
|
Pole (4-fold)
Equator
|
Symmetrical construction with 4-fold symmetry: 4+4+4+4, which is indeed optimum in the sense of “packing”.
Phi= 52.2443957°.
Symmetry type D4d (4-fold antiprismatic symmetry)
|
D16 / unk |
McTrivia / Shapeways |
|
Unknown design
Numbered to get the same results as throwing 2 D4s (8,7,7,6,6,6,5,5,5,5,4,4,4,3,3,2) |
D17 / D5h5-fold |
Magic / Shapeways
|
Pole (5-fold)
Equator
|
Symmetrical construction with 5-fold rotational symmetry: 1+5+5+5+1.
Phi=51.03° (almost optimum)
Symmetry type D5h (5-fold prismatic symmetry)
Numbered such that the sum of the 5 numbers of the two tropics and of the equator is constant (and equals to 51) and that the sum of the 2 poles, of two numbers of the tropics that are symmetric relatively to the equator, of two numbers of the equator that are symmetric relatively to number 9 is constant (and equals to 18) |
D17 / unk |
McTrivia / Shapeways |
|
Unknown design |
D17 / C2vOptimum 2-fold |
No design available yet |
|
Polyhedron consists of 1 rhombus, 10 pentagons and 6 hexagons
Optimum in the sense of “packing”.
Phi= 51.0903285°.
Symmetry type C2v=D1h (reflection in a plane and a 180° rotation through a line in that plane) |
D18 / Oh“Rhombi-cuboctahedron” 4-fold |
Magic /
Magic / Shapeways
|
Pole (4-fold)
Equator
|
Intersection of the squares of Rhombicuboctahedron and a sphere (there are 18 squares; the 8 triangles are not used)
Phi=45°=360°/8
Symmetry type Oh (full octahedral symmetry)
All faces are parallel.
Numbered such that opposite faces sum to 19 and that the 8 numbers around any of the 3 diameters sum to 76 (8 times the average value, which is 9.5) and that the 6 numbers surrounding a spherical zone to sum to 57 (six times 9.5).
|
D18 / D2h2-fold Optimum |
Shapeways
|
North Pole (2-fold)
Equator
South Pole (2-fold) |
Optimum in the sense of “antipodal packing”.
Phi= 47.9821°
Symmetry type D2h (prismatic symmetry)
All faces are parallel.
See this thread for more information. |
D18 / C2Optimum 2-fold |
No design available yet |
|
Polyhedron consists of 1 rhombus, 10 pentagons and 6 hexagons
Optimum in the sense of “packing”.
Phi= 49.5566548°.
Symmetry type C2 (2-fold rotational symmetry), no reflectional symmetry! |
D19 / unk2-fold |
Magic / Shapeways |
|
Designed based on minimum energy, but then maximized the radii. The repartition of the faces by layers is 1+4+2+4+2+2+4.
2-fold rotational symmetry.
Phi=?°.
Symmetry type unknown (C2?) |
D19/ unk |
McTrivia / Shapeways Missing |
|
Unknown design |
D19 / CsOptimum
|
No design available yet |
|
Polyhedron consists of 14 pentagons and 6 hexagons
Optimum in the sense of “packing”.
Phi= 47.6919141°.
Symmetry type Cs (reflection symmetry), no rotational symmetry!
This design has one rattler. |
D20 / Ih“Icosahedron”
|
Magic / Shapeways
|
Intersecting polyhedron
Constellation (dual)
Pole (3-fold)
|
Intersection of a regular icosahedron and a sphere. The 20 points form a pentagonal dodecahedron.
“Fair”, but not optimum.
Phi=41.810315°=2*arcsin(1/sqrt(3)/psi) where psi=(1+sqrt(5))/2, the golden ratio
Symmetry type Ih (full icosahedral symmetry)
All faces are parallel.
Due to the fact that a vertex is surrounded by 5 triangles, the rounded area is larger than in other truncated sphere dice (34.2%, about twice as much as average), yielding to smaller faces. |
D20 / D3hOptimum 3-fold
|
No design available yet |
|
Polyhedron consists of 14 pentagons and 6 hexagons
Optimum in the sense of “packing”.
Phi= 47.4310362°.
Symmetry type D3h (3-fold prismatic symmetry)
This design has two rattlers at the poles. It was found by van der Waerden in 1952. |
D21 / C1Optimum No symmetry |
No design available yet |
|
Polyhedron consists of 12 pentagons and 9 hexagons
Optimum in the sense of “packing”.
Phi= 45.6132231°.
Symmetry type C1 (no symmetry) |
D21 / unk |
Magic / Shapeways Not yet available
|
|
4-fold rotational symmetry, 4+4+4+4+4+1
these two arrangements of 21 circles around the sphere seem as efficient (the diameter of the circles is the same for a given sphere). |
D21 / unk |
Magic / Shapeways Not yet available
|
|
2-fold rotational symmetry 2+4+2+4+2+2+4+1 |
D22 / D5d |
Magic /
Magic / Shapeways |
Pole (5-fold)
Equator |
5-fold rotational symmetry, 1+5+5+5+5+1
Symmetry type D5d (5-fold antiprismatic symmetry)
Optimum in the sense of “antipodal packing”.
|
D22 / Td |
Magic / Shapeways |
Intersecting polyhedron
North Pole
South Pole
Equator |
Polyhedron consists of 12 pentagons and 10 hexagons
Optimum in the sense of “energy”.
Symmetry type Td (full tetrahedral symmetry).
Phi= 43.302°. |
D22 / unk |
McTrivia / Shapeways |
Top
Bottom |
Unknown design
Parallel faces |
D22 / C1Optimum No symmetry |
No design available yet |
|
Polyhedron consists of 12 pentagons and 10 hexagons
Optimum in the sense of “packing”.
Phi= 44.7401612°.
Symmetry type C1 (no symmetry) |
D24 / Oh“Deltoidal Icositetrahedron”
|
Magic / Shapeways
|
|
Intersection of deltoidal icositetrahedron and a sphere.
“Fair”, but not optimum.
Phi= 41.89055556°
Symmetry type Oh (full octahedral symmetry)
All faces are parallel.
Parallel faces, opposite faces sum to 25. |
D24 / O“Pentagonal Icositetrahedron” Optimum
|
Magic / Shapeways |
|
Intersection of pentagonal icositetrahedron and a sphere.
“Fair” and optimum in the sense of “packing”.
Phi= 43.6907671°
Symmetry type O (chiral octahedral symmetry)
No parallel faces. |
D25 / unk |
McTrivia / Shapeways |
|
Unknown design
Numbered to get the same results as
throwing 2 D5 (10,9,9,8,8,8,7,7,7,7,6,6,6,6,6, |
D28 / unk |
McTrivia / Shapeways |
Top
Bottom |
Unknown design
Parallel faces |
D30 / unk |
McTrivia / Shapeways Missing |
|
Unknown design
Alphabet, including spanish letters |
D32 / D3d3-fold |
Glass, made in Czechoslovakia |
|
Symmetrical construction with 3-fold rotational symmetry: 1+6+9+9+6+1.
Symmetry type D3d (3-fold antiprismatic symmetry)
Numbered 00,0,1..30 |
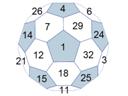
D32 / Ih“Nonuniform
|
Magic / Shapeways
|
Pole (29)
Equator (between 11 and 18)
|
Intersection of nonuniform truncated icosahedron (convex hull of the rhombidodecahedron), a kind of polyhedral soccer ball, and a sphere.
Optimum in the sense of “energy”, “covering”, and “volume”, but not “packing”.
Phi= 37.377°.
Symmetry type Ih (full icosahedral symmetry).
Numbered from 1 to 32 with the difference between two numbers on opposite faces being always 16. Taking the sum of a face surrounded by 5 neighbours (there are twelve of them, that orrespond to pentagons on the underlying polyhedron) and its 5 surrounding faces equas 99.
|
D32 / C3Optimum 3-fold |
No design available yet |
|
Polyhedron consists of 12 pentagons and 20 hexagons
Optimum in the sense of “packing”.
Phi= 37.475214°.
C3 (3-fold rotational symmetry) |
D33 / D3h |
Magic / Shapeways
|
Pole (center point between 6,12,33)
equator |
Symmetrical construction with 3-fold rotational symmetry: 3+9+9+9+3.
Symmetry type D3h (3-fold prismatic symmetry)
All faces are parallel.
Numbered such that all numbers are by groups of 3 that sum to 51:
All numbers sum to 34 by group of 2 (except obviously 17, since only 17 itself can sum to 17 to give 34):
- all the numbers of the equator (except 17) with their ymmetric number relatively at number 17 |
D33 / C3Optimum 3-fold |
No design available yet |
|
Polyhedron consists of 12 pentagons and 21 hexagons
Optimum in the sense of “packing”.
Phi= 36.254553°.
C3 (3-fold rotational symmetry) |
D36 / unk |
McTrivia / Shapeways |
|
Unknown design
Numbered like 2D6 |
D40 / unk |
McTrivia / Shapeways |
|
Unknown design
|
D50 / D6h6-fold |
Alan Davies |
|
Symmetrical construction with 6-fold rotational symmetry: 1+6+12+12+12+6+1.
Symmetry type D6h (6-fold prismatic symmetry)
Numbered 0 (empty),1..49 |
D50 / D4hWMF |
WMF
|
North pole
South pole
Equator |
Symmetrical construction with 4-fold rotational symmetry: 1+4+4+4+8+8+8+4+4+4+1
Symmetry type D4h (4-fold prismatic symmetry)
Numbered 1..49 plus symbol WMF (0 or 50). Used for German Lotto with numbers 1..49.
|
D50 / Oh |
friz / Shapeways Missing |
North pole
South pole |
Symmetrical design, based
Symmetry type Oh (full octahedral symmetry).
Roulette die, labelled 1, 2, 3, ..., 36, 0, 00, ODD, EVEN, HIGH, LOW, BLACK, RED, 1-12, 13-24, 25-36, Col 1, Col 2, Col 3. |
D50 / unk |
Magic / Shapeways Not yet available
|
|
This is a Truncated Sphere D50 based on a special polyhedron that is the intersection of a cube (6 squares), and octahedron (8 hexagons with a 3-fold rotational symmetry), a rhombic dodecahdron (12 hexagons with a 2-fold rotational symmetry) and a non-usual icositetrahedron (24 hexagons with a simple symmetry). You can check: 6 + 8 + 12 + 24 = 50.
|
D60 / unk |
McTrivia / Shapeways |
|
Unknown design
Numbered 0..59 |
D100 / imp“Zocchihedron” |
GameScience |
|
Symmetrical construction: 1+6+11+15+17+17+15+11+6+1
Symmetry type improper rotation / rotoreflection: Lower hemisphere is mirrored at equatorial plane and rotated by 360/34°.
Numbered 1..100
Zocchihedron is the trademark of the most common 100-sided die, which was invented by Lou Zocchi, and debuted in 1985. |
D144 / unk |
McTrivia / Shapeways |
|
Unknown design
|
Other spherical dice
D1 |
|
|
Truncated sphere with one circle at the south pole such that the die stops with a high probability with the “1” up. |
D4 |
|
|
Colours instead of numbers. Easier to roll than a tetrahedron |
![[Ref]](http://www.shapeways.com/openfilens/355544/photos/photo53015.jpg){kind=link}
![[Ref]](http://www.shapeways.com/openfile/250649/photos/photo39472.jpg){kind=link}